古典概型及其特征-概率论与数理统计

在例1．1．1中的E 1和E 4，它们具有两个共同特点：

（1）试验的样本空间只包含有限个元素；

（2）试验中的每一个基本事件发生的可能性相同．

具有以上两个特点的试验，称为古典型试验．

定义1．2．3（概率的古典定义）设随机试验E为古典型试验，它的样本空间为Ω＝｛ω1，ω2，…，ωn｝，事件A包含k个基本事件，则事件A的概率为

式中，k＝事件A包含的基本事件数，n＝Ω中基本事件的总数．

称满足定义1．2．3的概率模型为古典概型．显然，在古典概型中，基本事件发生的概率都相等，因此，古典概型又称为等可能概型．古典概型在概率论的产生和发展过程中是最早且最常用到的一种概率模型．

例1．2．2　将一枚硬币抛掷3次．（1）设事件A 1为“恰有一次出现正面”，求P（A 1）；（2）设事件A 2为“至少有一次出现正面”，求P（A 2）．

解　（1）“将一枚硬币抛掷3次”这个试验的样本空间为Ω＝｛HHH，HHT，HTH，THH，HTT，THT，TTH，TTT｝，而A 1＝｛HTT，THT，TTH｝．由于Ω中基本事件总数为8，这是古典概型问题，根据式（1．2．1），得．

（2）由于A 2＝｛HHH，HHT，HTH，THH，HTT，THT，TTH｝，所以根据式（1．2．1），得．

例1．2．3　将n只球随机地放入N（N≥n）个盒子中去，试求每个盒子至多有一只球的概率（设盒子的容量不限）．

解　将n只球随机地放入N（N≥n）个盒子中去，每种放法是一个基本事件．易知，这是古典概型问题．由于每一只球都可以放入N个盒子中的任意一个，故共有N×N×…×N＝N n种不同的放法．而每个盒子至多放有一只球，共有N×（N-1）×…×［N-（n-1）］种不同的放法．根据式（1．2．1），得所求的概率为

有许多问题和本例有相同的数学模型．例如生日问题，假设每个人的生日在一年365天中的任意一天是等可能的，即等于，那么，随机选取n（n≤365）个人，根据例1．2．3的结果（取N＝365），则他们的生日各不相同的概率为(www.xing528.com)

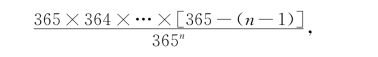
则n个人中至少有两个人生日相同的概率为

对n＝10，20，30，40，50，60，70，80，计算的结果见下表（MATLAB程序见本书附录B的例B．2．1）：

生日问题的概率曲线图（MATLAB程序见例B．2．1），见图1-7．

图1-7　生日问题的概率曲线图

由此可见，尽管一年有365天，任意30个人在一起，至少两个人同生日的概率就高达0．7063，这是我们意想不到的结果．故只凭直观想象不一定能作出正确的判断．

例1．2．4　设有N件产品，其中有M件次品，今从中任意取n件（抽取一个后不再放回），问其中恰有k（k≤M）件次品的概率是多少？

解　在N件产品中抽取n件，所有可能的取法共种（抽取一个后不再放回），每一种取法是一个基本事件，且由对称性知每一个基本事件发生的可能性相同．在M件次品中取k件，所有可能的取法共种．在N-M件正品中取n-k件，所有可能的取法共有种．根据乘法原理知，N件产品中取n件，其中恰有k件次品的取法共有种．根据式（1．2．1），得所求事件的概率为p．

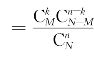如果取N＝9，M＝3，n＝4，则当k＝0，1，2，3时，p的计算结果见下表：

注　从n个不同元素中任取k（k≤n）个元素组成一组（不考虑元素间的先后次序），称为一个组合，此种组合的总数记，其计算公式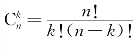，其中n！＝1·2…（n-1）·n．