频率与概率的统计定义

定义1．2．1　在相同条件下，进行了n次试验，在这n次试验中，事件A发生的次数n A，称为事件A发生的频数，比值n A n称为事件A发生的频率（frequency），并记作f n（A）．

根据定义1．2．1，易知频率具有下述基本性质：

（1）对于任意事件A，有0≤f n（A）≤1；

（2）对于必然事件Ω，f n（Ω）＝1；

（3）对于两两互不相容的事件A 1，A 2，…，Ak，有

即，两两互不相容事件的和事件的频率等于每个事件频率的和．

由于事件A的频率是它发生的次数与试验次数之比n A n，其大小表示事件A发生的频繁程度．因此，直观的想法是用事件A的频率表示事件A在一次试验中发生的可能性的大小，但是否可行呢？我们先看下面的例子．

例1．2．1　抛一枚质地均匀硬币的试验，历史上有人做过．设n表示抛硬币的次数，n H表示出现正面的次数，f n（H）表示出现正面的频率，得到表1-2的数据．(www.xing528.com)

表1-2　抛硬币试验

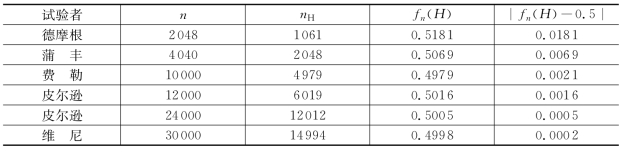
从表1-2中的数据可以看出，抛硬币的次数n较小时，出现正面的频率f n（H）在0与1之间波动相对较大．但随着n的增大，f n（H）呈现出稳定性，即当n逐渐增大时，f n（H）总在0．5附近徘徊，而逐渐稳定于0．5．

例1．2．1　说明，随机事件在大量重复试验中其结果呈现出某种规律性，而频率的稳定性正是这种规律性的表现．

在附录B中（例B．2．11）给出了用MATLAB软件模拟抛硬币试验及MATLAB程序．

定义1．2．2（概率的统计定义）在大量重复试验中，若事件A发生的频率稳定地在某一个常数p附近摆动，则称该常数p为事件A发生的概率（probability），记作P（A），即P（A）＝p．

应该指出，频率是变动的，而概率（频率的稳定值）则是常数．当试验的次数足够多时，频率相对稳定，可以把频率作为概率的近似值，即P（A）≈f n（A）．我们在日常生活中，经常说的产品的合格率、彩票的中奖率等，都是指频率．