在进行随机试验时,人们常常关心满足某种条件的那些样本点组成的集合,即“随机试验的某些样本点组成的集合”(亦即样本空间的子集).例如,若规定某种灯泡的寿命小于1000h为次品,则我们在例1.1.1的E 6中关心是否有t≥1000h,满足这个条件的样本点组成样本空间Ω6的一个子集{t|t≥1000}.
称试验E的样本空间Ω的子集为E的随机事件(或“随机试验的某些样本点组成的集合”),简称事件(event).在一次试验中,当且仅当这一子集中的一个样本点出现时,称这一事件发生.随机事件一般用大写字母A,B,C等来表示.
例1.1.2 在例1.1.1中,看几个事件的例子.对于E 2,事件“第一次出现H”,即A 1={HHH,HHT,HTH,HTT};事件“3次出现同一面”,即A 2={HHH,TTT}.对于E 4,事件“出现偶数点”,即A 3={2,4,6}.
特别地,由一个样本点组成的单点集,称为基本事件.例如,在例1.1.1的E 1中,有2个基本事件{H}和{T};在E 3中,有4个基本事件{0},{1},{2},{3}.
样本空间Ω包含所有样本点,它是自身的子集,在每次试验中它总是发生的,称为必然事件.
空集∅不包含任何样本点,它也作为样本空间的子集,它在每次试验中都不发生,称为不可能事件.
事件是一个集合,所以事件间的关系与运算自然按照集合论中集合间的关系与运算来处理.下面这些关系与运算的提法,是根据集合间的关系与运算以及“事件发生”的含义给出的.
设试验E的样本空间Ω,而A,B,Ai(i=1,2,…)是Ω的子集.
(1)若A⊂B,则称事件B包含事件A,这指的是事件A发生必然导致事件B发生.
若A⊂B且A⊃B,则称事件A与事件B相等,记为A=B.
(2)事件A∪B={x|x∈A或x∈B}称为事件A与事件B的和事件.当且仅当A,B中至少有一个事件发生时,事件A∪B发生.
类似地,称![]() 为n个事件A 1,A 2,…,An的和事件,称
为n个事件A 1,A 2,…,An的和事件,称![]() 为可列个事件A 1,A 2,…的和事件.
为可列个事件A 1,A 2,…的和事件.
(3)事件A∩B={x|x∈A且x∈B}称为事件A与事件B的积事件.当且仅当A,B同时发生时,事件A∩B发生.事件A与事件B的积事件,简记作AB.
类似地,称![]() 为 n个事件A 1,A 2,…,An的积事件,称
为 n个事件A 1,A 2,…,An的积事件,称![]() 为可列个事件A 1,A 2,…的积事件.
为可列个事件A 1,A 2,…的积事件.
(4)事件A-B={x|x∈A且x∉B}称为事件A与事件B的差事件.当且仅当A发生,B不发生时,事件A-B发生.
(5)若A∪B=Ω且A∩B=∅,则称事件A与事件B互为对立事件(或逆事件).记事件A的对立事件为 ,
, =Ω-A.
=Ω-A.
(6)若A∩B=∅,则称事件A与事件B互不相容(或互斥).这指的是事件A与事件B不能同时发生.显然,同一个试验中各个基本事件是两两互不相容的.
我们可以用维恩(Venn)图来表示上述事件间的关系与运算,如图1-1—图1-6所示.

图1-1 A⊂B

图1-2 A∪B
 (https://www.xing528.com)
(https://www.xing528.com)
图1-3 A∩B
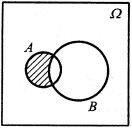
图1-4 A-B
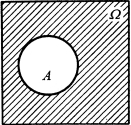
图1-5 
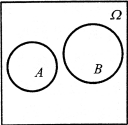
图1-6 A与B互不相容
在进行事件的运算时,经常要用到下述定律.设A,B,C,Ai(i=1,2,…,n)为事件,则有
交换律:A∪B=B∪A,A∩B=B∩A.
结合律:A∪(B∪C)=(A∪B)∪C,A∩(B∩C)=(A∩B)∩C.
分配律:A∪(B∩C)=(A∪B)∩(A∪C),A∩(B∪C)=(A∩B)∪(A∩C).
德摩根(De Morgan)律:
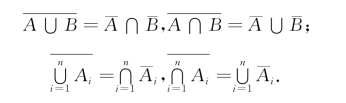
在集合论、概率论中符号与意义的对照,见表1-1.
表1-1 在集合论、概率论中符号与意义的对照

续表

例1.1.3 考察学生在一次数学考试中的成绩(括号中的区间表示成绩所处的范围),记A=“优秀([90,100])”,B=“良好([80,90))”,C=“中等([70,80))”,D=“及格([60,70))”,E=“未通过([0,60))”,F=“通过([60,100])”,则A,B,C,D,E为两两互不相容事件;E与F互为对立事件,即¯E=F;F=A∪B∪C∪D.
例1.1.4 对于例1.1.2中的A 1={HHH,HHT,HTH,HTT},A 2={HHH,TTT},求![]()
解 根据例1.1.1知样本空间为Ω2={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT},则A 1∪A 2={HHH,HHT,HTH,HTT,TTT},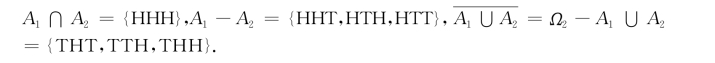
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




