分块算法生成高质量全息图

由于人眼的分辨率为0.175mm，即小于该距离的两点人眼便不能把它们区分开来，而会把它们视为一个点。在全息显示中为了做到既减少计算量又不影响成像质量，我们有必要充分利用人眼的分辨率极限对物波进行抽样，从而减少抽样数使计算量减少。我们在全息显示实验过程中使用的是德州仪器公司生产的数字微镜器件（DMD），该器件是由800×600个16μm×16μm的铝制微镜组成，相邻两微镜间的间隔为1μm。因此我们可以在物体所在的平面与全息图所在的平面分别采用不同的采样间隔，即物面根据人眼的分辨率极限进行采样，全息图所在的平面根据DMD微镜的尺寸大小进行采样。这样采样后我们就可以用一个像素较少的物体采用分块算法在全息面生成一幅像素较大的全息图，从而减少了计算量。对于旁轴近似下的菲涅尔衍射公式可写为：

式（4-7）又可写作

式（4-8）计算的复杂度为O（N2log2N2）。按照上述的采样方法式（4-8）可表示为：

其中，∆x0=∆y0=0.175mm，∆x=∆y=17μm，K=L。我们把物平面与全息图的坐标原点分别选在它们所在平面的中心，将全息图分成M个和原物体图像具有相同采样点数的块，如图4-3所示。原物通过菲涅尔衍射传播到全息面上M个与其像素数相同的相应区域。这样我们通过对原物的M次菲涅尔衍射计算即可算出物体传播到整个全息面的光场分布函数。设全息面被分的块数M=16，全息面的像2素数N=1024，则计算的复杂度降低为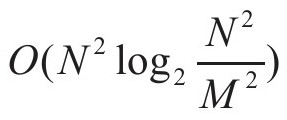，即计算的复杂度降为原来的60%。按照上述算法我们取一个256×256像素的物体，采用分块算法将一个1024×1024像素的全息面分成16个256×256像素的方块，经计算生成全息图，并通过DMD全息显示系统进行实验验证。为了提高全息图的衍射效率在计算过程中采用了二值化技术，图4-4是原始物体，图4-5是生成的全息图，图4-6是全息图经DMD重构后所生成的图像，图4-7是通过罗曼Ⅱ分数傅立叶变换系统所产生的全息图，图4-8是该种全息图通光DMD成像系统所再现出的图像。

图4-3　分块算法

图4-4　原始图像(www.xing528.com)

图4-5　全息图

图4-6　重现图像

图4-7　罗曼 Ⅱ型全息图

图4-8　罗曼图 Ⅱ型全息图的DMD再现

由图4-6与图4-8的比较可以看出在全息图再现时，采用菲涅尔分块算法生成的全息图的再现像的质量要好于采用分数傅立叶算法生成的全息图的再现像。由于函数的分数傅立叶变化与其菲涅尔衍射在菲涅尔区具有等价性，因此在计算分数傅立叶全息图时可以采用分块菲涅尔算法。