低测量次数下的快速、稳定、精确重构算法

CS理论框架的第三个核心内容是重构算法，要求算法在使用较少的测量值下，快速、稳定、精确重构原始信号。由于Φ的维数M远远小于x的长度N，这表明方程组中未知数的个数多余方程的个数，这是一个欠定方程组的求解问题。从方程的表面来看，这样的方程有无数个满足方程要求的解。但是，由CS理论使用的前提条件信号是可压缩的，从根本上解决了这一问题，使得欠定方程组有最优解，而且由压缩感知理论第二个核心内容，因稀疏分解字典和测量矩阵是不相关的或者测量矩阵满足有限等距性质，这就保证了从M个测量值中能够精确重构原信号。

为更好地解释压缩感知理论中信号重构的问题，首先引入范数的基本定义，假设向量X={x1，x2，x3，…，xn}，则X的lp范数可以表示为：

当p=0时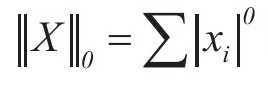，表示X中所有非零元素的个数；当p=1时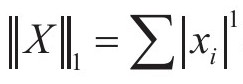，表示X中所有元素绝对值的和；当p=2时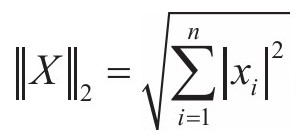，；且有p=∞，。

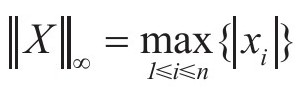因此，当信号x满足可压缩条件时，式（3-2）欠定方程组的求解转化为求最小l0范数解的问题。

对于该问题的求解需要列出所有满足式3-9要求的稀疏解才能找到最稀疏的形式，这是一个病态问题。为何式（3-9）的求解会出现一个稀疏解的问题我们利用几何图形进行分析，如图3-5所示。首先我们知道式（3-9）在几何图上的意思就是要求直线H上找一点，使其满足lp球的半径最小，观察图3-5（a），当0＜p＜1时，当球的半径逐渐增大时，首先与直线相交的点在轴线上，该点为式3-9的解，而且是最稀疏的解；观察图3-5（b），其为p=1的情形，该球变成一个菱形，当其也逐渐增大时，其效果与0＜p＜1时一样；观察图3-5（c），其为p＞1的情形，此时的球变为一个凸球，当其逐渐增大时，虽然与直线H也有交点，但是交点不在轴线上，所以得到的解是不稀疏的解，这不是我们想要的解，图3-5（d）是它的一个特殊情况。因此我们将最小l0范数解的问题转换为求最小l1范数解。那么有

图3-5　最小化l1范数有稀疏解的几何说明(www.xing528.com)

对于上述将目标函数进行转化，变为更为容易求解问题的方法我们称为凸松弛法，属于该类方法的算法有：基追踪法、迭代硬阈值法等，该类算法虽然重构的速度慢，但是在测量矩阵满足要求时，其在较少测量数的情况下仍能精确重构所有稀疏信号。这是压缩感知理论四类重构算法中的第一类方法。其余三类方法分别是贪婪算法、组合算法、统计类优化算法。

贪婪算法[3]主要包括正交匹配追踪算法（OMP）、梯度追踪、共轭梯度追踪等。该类算法的思想源于信号稀疏分解，它虽然需要测量数据多，且重构精度不高，但是它们计算的速度非常快，而且随着改进算法的不断提出，其重构精度有了很大改善。

组合算法主要包括链追踪算法、HHSP追踪算法、稀疏傅立叶描述法。该类算法主要针对信号进行高度结构化采样，再由群测试来快速获得信号支撑的思想。组合算法虽然只给出了在测量次数一定的条件下，可以高概率地获得任何可压缩信号重建的保证，而不是精确保证，但是其所需要的测量次数比凸优化算法还少，信号重构的速度也比较快。

统计类优化算法是我们平时不常用的，其主要包括两类：一类是贝叶斯类的统计优化算法，另一类是基于训练集合学习的稀疏重建算法。该类算法与统计学中的主成分分析法或者独立成分分析法相类似，利用典型的训练集通过不断学习来找到最优的线性投影集合。其优点是不仅能够精确保证重构的精度，而且需要的时间比凸优化算法短，但是测量次数较凸优化算法多。