信号稀疏表示及字典制作与稀疏能力分析

CS理论要求我们，被处理的信号x必须是稀疏的或者在某种变换下转为稀疏的形式。然而我们通常采样的对象本身并不是稀疏的（某一场景图像），这就要求我们如何将采样的信号转换为稀疏的情况。我们知道不稀疏的信号在某个稀疏字典下是稀疏的或者只有相对其中k个数比较大，那么，对稀疏字典的设计成为压缩感知使用过程中的核心问题之一。因为只有选择了合适的稀疏字典，才能满足原信号稀疏性要求，才能在较少的测量值下近似完整地重构原始信号。

迄今为止，稀疏字典的设计主要包括三种。第一种，某个正交基字典。通常我们选用的正交基是DCT正交基，Wavelet正交基和傅立叶变换正交基。第二种，紧框架字典。这类字典主要以Ridgelet, Curvelet, Bandlet, Contourlet为代表的图像几何分辨率表示或者称Beyond Wavelet变换。第三种，过完备字典。该类字典与正交基字典不同，它不再是单一的基作为字典，而其可能由多个基字典构成或者通过学习和构造得到冗余的原子库，通过增加字典中的原子来提高对图像等复杂信号的更好表示。下面就具体分析常用的第一种和第三种字典的制作和稀疏表示能力。

3.1.1　正交基字典分析

信号可压缩的标准是：其存在一个正交基B使得信号x可以被表示为x=Bθ，且θ=θk+w，其中θk是k稀疏的一组向量，w表示很小的量级。常见的正交基有离散余弦（Discrete Cosine Transform, DCT）正交基、离散Wavelet正交基、FFT正交基。

（1）离散余弦正交基构造

回忆一个一维离散的余弦变换由一个长度为n的时间信号{x（i），i=0，1，2，…，n-1}，去产生一个长度为n的序列{c（k），k=0，1，2，…，n-1}，该序列可表示为：

其中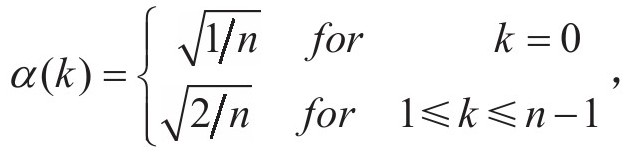：基于式（3-1）我们可以根据它的第k行构造一个正交基Cn。其第k行的表示式为：

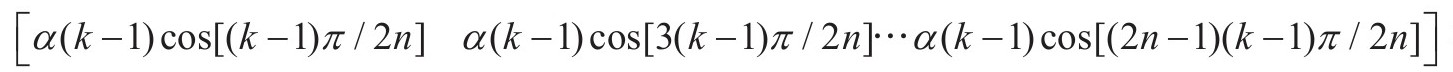根据上述理论，编写了MATLAB仿真程序来进一步验证DCT正交基的有效性，选取了一幅64pixel×64pixel大小的图像，如图3-1（a）所示，其像素大小分布如图3-1（b）所示，发现其并不是稀疏的，但经DCT正交基表示之后发现其只有很少一部分是相对较大的，所以通过设定阈值（本文选取的是50），使得在阈值之下的都为零，发现只有97个数不为零，其图像分布如图3-1（d）所示，再通过这97个非零数构成的向量与DCT正交基的转置相乘得到原始图像的再现像，如图3-1（c）所示，观察该图发现依然可以辨认图像内容，但原图像比较模糊。

图3-1

图3-1　DCT正交基下稀疏重现效果

（2）DWT正交基构造

由文献[1]可知离散的小波系数可以表示为：

而离散小波的重构式为：

式（3-2）和式（3-3）中f（t）表示平方可积的信号，ψj,k（t）表示离散的小波，Cj,k表示离散化的小波系数，C为一常量。

在分析了离散小波变换的基本知识后，我们假设信号的长度为n=2p，p为整数，那么n×n的离散小波基W可以采用的是Daubechies D8 Wavelet通过MATLAB的工具包产生。(www.xing528.com)

为了能够与DCT正交基进行比较，同样选择了一幅64pixel×64pixel大小的图像，其像素大小分布如图3-2（b）所示。观察发现其不是稀疏的，但经DWT正交基表示之后发现其只有很少一部分是相对较大的，所以通过设定阈值（本文选取的是50），使得在阈值之下的都为零，发现只有564个数不为零，其图像分布如图3-2（d）所示，再通过这564个非零数构成的向量与DWT正交基的转置相乘得到原始图像的再现像，如图3-2（c）所示，观察该图发现整个图像轮廓比较清晰，但主体残缺。

图3-2　DWT正交基下稀疏重现效果

为了进一步验证DWT正交基的优越性，我们选取了常规图像512pixel×512pixel的house图像，如图3-3（a）所示，进行试验比较。图3-3（b）是小波三层分解的结果，观察图像大部分是黑的，这说明其非常接近于零，它是非常稀疏的。图3-3（c）为图3-3（b）的再现图像，观察整个图像显示很清楚。

图3-3　二维DWT正交基稀疏效果比较

3.1.2　过完备字典构造

过完备字典是通过反映不同种类图像特征的原子模型构成，其原子不再是单一的基函数，而是一个过完备原子库冗余系统。构造过完备字典时要求尽可能包含时频特性，以更好地体现不同图像的不同特征，对字典中的单个原子进行平移、伸缩、旋转、调制就可以生成过完备原子库。一类构建过完备原子库的方法是通过不同的完备字典组合而成，而这些完备字典可以是Contourlets字典、小波字典、离散余弦字典、Curvelets字典、傅立叶变换字典等。通过组合这些字典使得新字典中能够表示原信号的原子更为丰富，这样所表示出的结果就更为简洁，也就是稀疏性更好。与前一种构造过完备字典的方式不同，我们知道要想更好的反映一幅图像的特征，通过其自身训练出的字典是最完美的，其包含图像的信息更完整，为此能够更准确地稀疏表示原图像。该类算法包含两步：①用固定的字典对图像进行展开；②根据展开的系数进一步更新原子库。

2006年，Michal Aharon等人在K-means聚类算法的基础上，提出了K-SVD设计过完备字典稀疏表示的算法。它在图像样本的基础下，通过稀疏分解系数不断迭代更新原有字典的原子，使得到的过完备原子库更能准确地反映图像的特征。而且，在K-SVD算法调整字典的同时，图像稀疏分解的性能也在逐步提升，这样加快了算法的收敛和分解速度。基于K-SVD过完备原子字典稀疏表示的算法主要步骤为：

假设，初始过完备原子库为D∈Rn×K，训练信号y∈Rn，训练信号的稀疏表示向量xR∈K，N个训练信号的集合可以表示为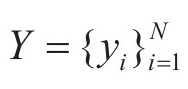，Y解的向量集合为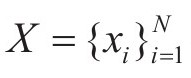，其中Rn表示n维的信号。K-SVD的首要任务是使用任意的追踪算法对每一个训练信号yi去计算表示向量xi，通过近似解决式（3-4）完成。

其中：T0表示解向量稀疏xi中非零向量的最大个数。第二任务是迭代训练更新原子库D。设原子库的第k列向量为dk，则原信号集可以分解表示为：

其中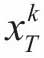：为dk对应系数矩阵X的第k行向量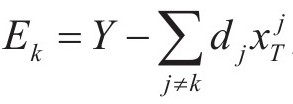，为不包括dk的信号集Y的分解误差。为应用SVD分解，定义集合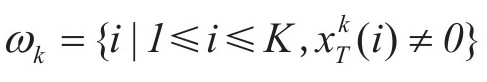为信号{yi}分解中用到dk时所有yi的索引所构成的集合，定义Ωk为N×|ωk|矩阵，它在（ωk（i）,i）位置上的元素都为1，而其余位置皆为0。则有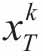，Y,Ek在去掉零后收缩结果为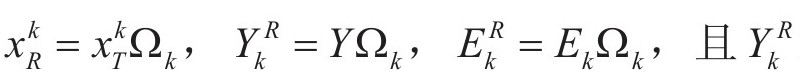为当前用到原子dk的样本集合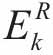，为不包括原子dk影响的样本所产生的误差值。此时式3-5可以转化为：

其中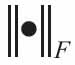：为矩阵的Frobenins范数。将Ek进行SVD分解得到Ek=U∆VT，其中U的第一列为dk是dk的优化结果。此时，D中的一列更新结束，按照上面的方法将D逐列进行更新，最后训练出一个新的字典。

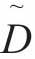在分析了K-SVD设计过完备字典稀疏化的算法之后，编写了相关MATLAB程序对其进行仿真实验，选取大小为512pixel×512pixel的peppers作为原始图，如图3-4（a）所示，并选用四幅其自身图像训练出来的字典如图3-4（b）所示，最后用过完备稀疏字典恢复出的图像如图3-4（c）所示，观察比较图3-4的（a）和图3-4（c）发现完全一样，采用相关系数比定量比较，其相关系数为1。

图3-4　K-SVD过完备字典稀疏效果比较