计算全息与图像加密中的典型全息编码

2.4.1　迂回位相编码

2.4.1.1　迂回位相编码理论

科学家在做光谱分析时发现，如果光栅常数误差较大时光谱线旁侧会出现假线，即鬼线（ghost line），这一度使科学家感到困惑和苦恼。然而鬼线的出现并不总是坏事，Brown和Lohman对此现象进行研究提出了迂回相位的概念和理论并将其和计算机科学相结合制作出了世界上第一张计算全息图，开创了计算全息的先河。

当用平面波垂直照射到规则的光栅即有固定光栅常数的光栅上时，经光栅衍射后不同衍射级的光传播到不同方向，就同一衍射级而言，相邻狭缝的衍射光的光程差为一个波长的整数倍，相位差为2π的整数倍，衍射光是一束束直的平行线且每束光之间的间距相等，与此衍射波传播方向垂直的平面具有相同的相位，即为等相位面。如果光栅不规则，垂直照射到该光栅上的光经衍射后各衍射级的衍射光线不再是直的、不再是平行的，间距也不再相等，从而产生了相位的延迟或超前，这些偏离原衍射级的光线被称为“鬼线”。

如图2-7所示为一不规则光栅，设光栅规则时的光栅常数为d，该光栅在某一位置的光栅常数增大或减少的量为d’。由光栅方程可知，当平面波垂直照射到光栅常数为d的光栅时，在衍射角为φm的第m级衍射中，相邻光线的光程差满足方程

当某一位置的光栅常数为d+d’时，该处在φm方向上相邻光线的光程差为

在φm方向衍射光波的相位延迟为

图2-7　不规则光栅的衍射

这种由光栅狭缝的错位导致的位相偏移φm被称为迂回位相。由不规则光栅的错位栅缝的衍射光和同一衍射方向的其他光波在位相上的差异效应称为迂回位相效应。迂回位相的值仅与光栅的错位量d’有关，而与其他量无关，因此要在某一特定方向得到所需的位相只需获得相应的光栅错位量d’即可。

2.4.1.2　Lohmann迂回位相编码

Ⅰ.迂回位相编码方法

Lohmann等人根据迂回位相效应对物函数进行编码制作出了只有“1”透光和“0”不透光的所谓的二元计算全息图。全息图被抽样为一个个正方形的抽样单元（cell），每个单元内放置一个通光孔，通光孔的形状可以根据需要进行选择，在Lohmann编码中所选择的通光孔为矩形，通光孔的高度与该抽样点物波函数的振幅成正比，每个抽样点的位相则是根据迂回位相效应改变通光孔中心与其所在单元中心的距离来表示的。这样对于空间的复振幅函数的振幅和相位就可以用两个非负的实函数分别表示，通过这种方法制作的全息图相当于一个只有0和1透过率的不规则的光栅。图2-8所示为迂回位相编码全息图的第（m,n）个抽样单元的编码，图中深颜色的正方形为抽样单元，其边长δfx=δfy，抽样单元内白色矩形为通光孔，Bmn为通光孔的宽度是一个常量，Hmn为通光孔的高度，dmn为抽样单元中心与通光孔中心的距离。

图2-8　迂回位相编码全息图的第（m,n）个单元

Ⅱ.傅立叶变换全息图的迂回位相编码

全息图由一个个抽样单元组成，每一抽样单元内有个矩形通光孔，根据迂回位相编码第（m,n）个抽样单元的透过率函数可写为

整个全息图的透过率函数可写为

其中rect（）为矩形函数，。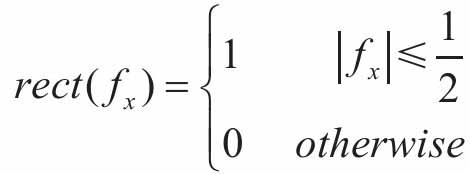

用平面波exp（j2πx0fx）照射该全息图，再对出射光进行傅立叶逆变换可得

设物函数为f（x,y）=A（x,y）exp[jφ（x,y）]，其频谱函数F（fx，fy）离散形式为Fmn=Amnexp（jΦmn），用内插公式

其中∆X、∆Y分别为物函数在空间坐标中的x轴与y轴方向的尺寸，且1/∆X=δfx，1/∆Y=δfy。对（2-36）进行傅立叶逆变换就可得到f（x,y）的离散表达式

要对物函数的频谱进行准确的编码必须要使式（2-34）与式（2-37）相等以找出编码的规则。在sin c[Bmn（x+x0）]常数，sin c（Hmny）=1，

exp[j2πx（mδfx+dmn）]=1的情况下令（2-34）与（2-37）相等，并结合最佳亮度时Bmn的取值，最后得出编码规则

Ⅲ.模式溢出问题及解决方法

模式溢出问题是迂回位相编码的一个极为重要的问题，下面分三种情况来讨论这一问题。如图2-9所示，设编码单元为边长δfx的正方形，中心坐标为（x0y0）；通光孔的宽为Bmn=δfx/2，高为H，中心坐标为（x’0，y’0）。

（1）如图2-9所示，当相位角Φmn满足：0≤Φmn≤π/2，即抽样单元中心与相应的通光孔中心的距离dmn满足：0≤dmn≤δfx/4时，x’0-x0=dmn⇒x’0=dmn+x0。设矩孔左、右边的横坐标分别为x1，x2，纵坐标分别为y1，y2，则x1=x’0-Bmn/2=dmn+x0-Bmn/2，x2=x’0+Bmn/2=dmn+x0+Bmn/2，y1=y0-Hmn/2，y2=y0+Hmn/2。

（2）当π/2＜Φmn≤3π/2，即δfx/4＜dmn≤3δfx/4时，有溢出一部分在抽样单元中心的右侧，另一部分在抽样单元中心的左侧。x1左=x’0-Bmn/2=x0+dmn-Bmn/2，x2右=x0+δfx/2，x’1左=x0-δfx/2，x’2右=x’1左+Bmn-（x2右-x1左）=x0-δfx/2+Bmn-（x0+δfx/2-x0-dmn+Bmn/2）=x0+dmn+Bmn/2-δfx。

（3）当3π/2＜Φmn≤2π，即3δfx/4＜dmn≤δfx时，dmn-3δfx/4=∆，x1=x0-δfx/2+∆，x2=x0-δfx/2+∆+Bmn

图2-9　模式溢出问题解决方法

（a）相位角满足0≤Φmn≤π/2时的编码。（b）通光孔，（c）相位角满足π/2＜Φmn≤3π/2时的编码。（d）相位角满足3π/2＜Φmn≤2π时的编码。

由于罗曼迂回编码的抽样单元为一个个方格，故其结构与DMD的方块形像素相似，于是我们首先采用改进的迂回位相编码方法进行全息显示的研究。

2.4.2　位相迭代全息

迭代相位恢复算法的原理是在已知光波光强分布的条件下，利用迭代恢复求解光波的相位信息。一般的思路是任意给定一输入面上的初始相位，将迭代获得的恢复图像与原始图像进行对比，如果小于预先设定的阈值则保留此次迭代结果，否则，调整相位进行下一次迭代。初始相位的选择是随机的，迭代的次数一般满足均方误差大小的约束条件即可。

2.4.2.1　两面之间的数值迭代法

由于傅立叶变换形式和计算量的简单，因此在这节中，为说明迭代型相位恢复算法的基本思想，就用傅立叶变换作为光波的传输方程。则其基本示意图如图2-10所示。

图2-10　两面数值迭代流程

图2-10中，x1-y1为输入平面，x2-y2为输出平面。从图中看出其基本算法流程，首先给定一个初值U1（x1，y1），通过角谱传输方程计算出输出面的复振幅分布（此处选用的是傅立叶变换）U2（x2，y2），利用测量得到的强度H2（x2，y2）来修正U2（x2，y2），然后利用逆傅立叶变换回传到前一个平面，得到U1（x1，y1），同样用测量得到的强度H1（x,y）来修正U1（x1，y1），回到U1（x1，y1）完成一次迭代。所有的两平面迭代都遵循此流程，但不同的算法区别在于振幅的约束方式，下面将介绍GS及其改进算法，说明它们之间的异同。

Ⅰ.GS算法

GS算法是迭代相位恢复算法中的鼻祖，之后的算法都是在其基础上改进和发展起来的。它的核心思想是分别在空域和频域施加约束条件，使信号在物面和频谱面来回迭代地进行傅立叶变换，以达到最大限度恢复相位的目的。具体的流程如图2-11所示。

图2-11　GS算法流程

GS算法的具体步骤是：

（1）给定空域上的初始相位分布值φ（x,y），0≤φ≤2π。

（2）Gz（ξ,η）=FT[gz（x,y）]=|Gz（ξ,η）|exp[iΦz（ξ,η）]，对步骤（1）中的估计值进行傅立叶变换，得到频谱面的估计值。

（3）G'z（ξ,η）=|G（ξ,η）|exp[iΦz（ξ,η）]，对频谱面施加约束，用频谱面的振幅替代（2）中的振幅，相位保持不变。

（4）g'z（x,y）=IFT[G'z（ξ,η）]=|g'z（x,y）|exp[iφz'（x,y）]，对步骤（3）得到的估计值进行傅立叶反变换，得到一个物面估计值。

（5）gz+1（x,y）=|g（x,y）|exp[iφz'（x,y）]，同理，对物面施加约束作为新的估计值进入迭代循环。

（6）重复步骤（2）～步骤（5），随着迭代次数的增加，输出图像渐渐收敛于输入图像，当满足收敛准则时，结束迭代过程。此时空域得到的相位就是期望获得的相位信息。

GS算法通过设定约束条件，利用循环迭代不断优化找出它的可行解。因为迭代算法固有的缺陷，GS算法在进行过程中可能会停滞不前，因此，GS算法未必获得想要的结果。许多学者在GS算法的基础上不断改进，推出了许多更加精准的相位恢复方法。

Ⅱ.ER和HIO算法

ER和HIO算法是Fienup为解决GS算法收敛速度慢、受初值影响严重的问题而在其基础上改进的算法。

误差减少（ER）算法也是在输入面与输出面之间的迭代，但是舍去了输入面强度的检测要求。其流程和GS一样，区别在于上述的步骤（5）。根据输出面（物体域）的约束条件保留相位，更新物面的复振幅为

式中：k为统计迭代次数的变量，γ表示与物体域不符合的点集。在迭代过程中，物体域的振幅修正既可以是正性约束条件，又可以是支持域约束条件。

混合输入输出（HIO）算法的区别也是在同样的步骤中。在物体域的修正条件中加入了弛豫因子β，通常0.5≤β＜1。(www.xing528.com)

根据输出面（物体域）的约束条件保留相位，更新物面的复振幅为：

Ⅲ.反馈迭代（IFA）算法

反馈迭代算法是安徽大学的刘凯锋等人在全息领域中为降低重构噪声，提高全息图再现质量而提出的。该算法也是基于GS算法的改进，只是在输出面上对振幅的约束采取了比例反馈控制器，具体约束形式如下：

式中：α为比例反馈系数，在（0～1）之间。从中可以看出，对下一次迭代所使用的振幅并不完全是其测量值，而是利用测量得到的振幅和目前迭代出的振幅之间的差异作为对测量振幅的修正。

为说明以上各类算法的可行性和有效性，在此利用MATLAB对其进行模拟仿真，所使用的参数为：物体的大小为5cm×5cm，采样点数为512×512，输出面与物体的间距为0.3m，输出面的采样间距与输入面满足香农采样定理。图2-12是迭代次数为25次实验结果：

图2-12（a）、（b）分别为物光（输出面）的振幅和相位，图2-12（c）为输出面上检测的光强；图2-12（d）、（f）两张图就是利用原始振幅和输出面的强度作为迭代约束条件得到的重构相位分布，其效果相差不大，只是IFA有更快的收敛速度；图2-12（e）是ER算法的相位恢复结果，由于ER算法只利用输出面的强度作为约束条件，因此所用的信息没有GS、IFA算法多，重构出的相位自然比较差，但实际中物光强度难以检测，所以ER算法更具实用性。

图2-12　几种相位恢复算法的仿真结果

2.4.2.2　多平面之间的迭代

上文中提到的所有数值迭代法用来恢复光波的相位，都是根据两个面的强度信息，在两面之间来回迭代计算，虽然后三者在GS算法上有所改进，但实际的效果并不理想，易陷入局部极小点、抗噪性能差的缺点没有从根本上改变，收敛的速度提高不显著。而且当输入面是物光波本身时，检测输入面的强度分布则更加困难，况且物体的轮廓，即入瞳形状不可能精确地估计，使得在输入面上可以利用的强度信息就非常少。为解决这个问题，避免直接测量物光波本身，用三个或者更多的面进行循环迭代就成为比较明晰的思路。Laurent Bruel借鉴了GS迭代的思想，理论分析了多面循环迭代在相位恢复的应用。只要选择合理的输出面的位置，三个面得到的结果就是唯一的，并且相比于两面之间的迭代收敛速度大幅提高。这为多面迭代提供了理论基础。下面设计了一种对面迭代算法用以恢复复杂光场的相位分布，下面将系统地阐述多面迭代的过程。

如图2-13所示，物光小猴发出的光波沿着水平方向传播，在菲涅尔衍射区分别取如图2-12的5个平面，可利用CCD测量出这5个面的强度分布，分别为I1，I2，I3，I4，I5。现在的问题是，已知这5个平面上的强度信息，如何计算得到物光的复振幅。

图2-13　多面迭代

上图中，被选中的测量平面被分为两组，第一幅和第二幅在一起，靠近物光源近一些，而后三幅平面在一起，离物光源远一些，这样做的依据可以从强度传输方程（TIE）得到：在菲涅尔衍射区的近场，对物光相位分布的高频信息比较敏感，在菲涅尔衍射区的远场（夫琅禾费衍射区），则对物光相位分布的低频信息比较敏感。在图像处理领域中我们知道，图像的低频成分是变化缓慢的成分，可认为是图像的“轮廓”，高频反映了图像的细节信息。因此，在此例中，相位恢复分为两个步骤，第一步，用I3，I4，I5这三个强度分布进行数值迭代，恢复出物光波相位的轮廓；第二步，用近区的I1，I2强度分布进行数值迭代，恢复出物光波的细节信息，如图2-14所示。

图2-14　多面数值迭代的算法流程

图2-14中的FD和IFD表示菲涅尔衍射方程以及其逆向衍射方程，在传播到对应平面的时候，就用检测到的振幅来替换计算得到的振幅并保持相位不变。物光的初始相位全部设置为0，振幅设置为0～1上的均匀分布。从流程图中可以看出，左边的一侧迭代出相位分布的低频信号，最后用迭代的结果作为右边迭代的初始值，两次迭代时控制算法结束的价值函数仍为相邻两次迭代物光振幅的均方根误差（RMSE）。

为验证上述算法的有效性，利用matlab模拟仿真对其有效性进行验证，实验的参数为，物体的大小为5cm×5cm，采样点数为512×512，五幅平面到物面的距离分别为0.06m，0.12m，0.5m，1m，1.5m。按照流程图2-14进行迭代，得到的结果如图2-15所示。

图2-15　多面迭代的仿真结果

图2-15中（a）、（b）为构造的物波分布，用这两幅图作为物波的强度和相位。图2-15（c）～（g）为在五个不同位置的平面检测到的强度分布。图2-15（h）、（i）分别为远场中的三幅强度作为迭代约束条件迭代8次的重构结果，对应流程图2-14的第一环节，图2-15（j）、（k）是上面远场迭代的结果作为近场迭代的初值，利用检测的强度再次修正的结果，迭代也是8次，相比较可知，图2-15（h）、（i）表现的信息量没有图2-15（j）、（k）的丰富，尤其是相位分布，图2-15（k）比（i）体现了更多的细节信息。图2-15（l）、（m）是利用近场两幅强度迭代25次的结果，相比于图2-15（j）、（k），迭代次数变多，恢复的效果很差，这足以说明利用远场迭代恢复“轮廓”的必要性。但是无论如何，相比于两面的迭代，其相位恢复效果都要好得多，以下是多面迭代优点的总结：

（1）迭代的收敛值唯一并且是全局最优解，不像GS迭代中，可能因不同的初始值而产生不同的收敛结果。

（2）虽然在每一次迭代过程中计算量比较大，但是由于多平面的约束使得收敛速度极具加大，总体的计算量反而变小。

（3）两面的迭代算法对物光的要求比较高，必须是强度分布比较简单，相位变化平缓的物光，对于复杂的光场却很难恢复，但多面迭代可以恢复出结构复杂的光场。

（4）GS以及其他形式的两面之间的迭代算法，其前提条件是物光波的可测性，这在实际中很难实现，而多面迭代就不需要测量物平面的光波强度，其实质是既恢复了相位，又恢复了振幅。

2.4.3　纯相位型编码

2.4.3.1　纯相位型迂回位相编码

纯相位全息图因其衍射效率高、衍射级少而备受关注，理想情况下其衍射效率可达到100%。目前，纯相位全息图已被广泛应用于全息显示、滤波器、只读存储、干涉测试等领域。该全息图主要由计算机产生然后以浮雕的形式记录在胶片上或刻蚀在晶体上，然而这些记录材料一旦被记录后不可再重复使用，而且制作过程繁杂，对于全息显示来说极为不利。我们采用Gerchberg-Saxton生成纯相位的物波函数，然后用迂回位相编码对其进行编码生成计算全息图，该全息图可以很容易地通过计算机或一些移动设备进行存储、复制，摆脱了晶体或胶片局限性，而且比常规的迂回位相编码产生的全息图衍射效率要高。

采用Gerchberg-Saxton迭代算法生成纯相位物波函数后，我们将用罗曼的迂回位相编码方法对其进行编码，在用罗曼编码时采用多个通光孔进行编码。由于物波函数是纯相位的，因此在编码时通光孔的高度和抽样单元格一样，这样增加了光的透过率。根据罗曼编码方法每一抽样单元的透过率函数可写为

整个全息图的透过率函数为

采用上述方法即可制得所需的全息图。我们用一个64×64的汉字“安”作为原始图像，如图2-16（a）所示，生成的全息图如图2-16（b）所示，将编码后所获得的全息图输入DMD全息显示系统，经DMD调制后衍射即得到如图2-16（e）所示的再现图像。图2-16（c）是我们采用传统罗曼编码所得的全息图，图2-16（d）是将全息图2-16（c）输入DMD全息显示系统后再现出的图像。比较图2-16（d）和图2-16（e）可以看出，采用纯相位编码再现出的图2-16（e）较采用传统罗曼编码再现的图像2-16（d）在衍射效率上明显提高，而且图2-16（e）无零级衍射出现。

图2-16　典型罗曼编码与纯相位罗曼编码的比较

2.4.3.2　纯相位型余弦二值编码

在采用迂回位相编码及其改进的算法进行编码时由于要考虑模式溢出问题，因此在编码时要用多个像素表示一个抽样单元，这样就会造成像素的增加，因而对于像素较大的原始图像而言会产生比原始图像大得多的全息图，故不适合大像素原始图的全息制作与显示。通过对已有算法及物波函数构造的研究我们提出一种简单有效的编码方法，我们称其为余弦二值编码方法，该方法适合大像素图像的全息图制作与显示，而且能够从理论上消除多衍射级问题。具体实现过程为先采用迭代算法生成纯相位物函数再用我们提出的编码对其进行编码，最后采用我们全息显示系统进行显示验证。

假设我们想要得到的衍射模O（fx，fy）的振幅已知，其调制函数f（x,y）是振幅为1的纯相位调制函数。为了使调制函数f（x,y）包含物波的全部信息，我们采用相位恢复算法中的误差减少算法，在O（fx，fy）和f（x,y）之间进行迭代恢复出f（x,y）的相位。具体过程如下：

（1）由物函数得到想要的衍射模O（fx，fy）；

（2）由O（fx，fy）傅立叶逆变换得到纯相位函数f（x,y）；

（3）由f（x,y）傅立叶变换得到F（fx，fy）；

（4）把F（fx，fy）的振幅替换为O（fx，fy）的振幅得到F’（fx，fy）；

（5）对F’（fx，fy）进行傅立叶逆变换得到f’（x,y）；

（6）对f’（x,y）进行限制使其振幅为1得到f（x,y）；

（7）对f（x,y）进行傅立叶变换得到F（fx，fy）；

（8）重复（4）到（7）的步骤直到步骤（7）的幅值与想要的幅值满足某种方差要求。

对于纯相位的波函数f（x,y）可以令其等于eiθ（x,y），用欧拉公式将其展开为：

对于f（x,y）的共轭像可用欧拉公式展开为：

由上述两个式子可得

由（2-47）式可见cosθ中包含纯相位波函数与其共轭波函数两项，所以如果我们对cosθ进行二值编码，则编码后的图中只含有纯相位波函数与其共轭波函数而没有零级项。所谓二值编码，就是把物波函数编码成只有黑白两种灰阶的全息图，即全息图的透过率函数的取值为0或1。因为cosθ的函数值关于角度θ所在的坐标轴对称，所以我们可以很方便地将θ轴上方的函数值作为一个灰阶，θ轴下方的函数值作为另一个灰阶，即θ轴上方各离散点的灰阶值取为1（0），θ轴下方各离散点的灰阶取值为0（1）。即有

如果cosθ＞0，则cosθ=1；

如果cosθ＜0，θ则cosθ=0。

经过上述的余弦二值编码后我们可以得到如图2-17所示的全息图。我们以1024×1024像素的杯子作为原始图像，采用误差减少算法进行迭代生成纯相位物函数后，再用上述的余弦二值编码生成全息图并用计算机进行模拟重构得到很好的结果。原始图像、由原始图像生成的全息图、由全息图用计算机模拟重现的图像分别如图2-17～图2-19所示。图2-20为图2-18经我们的全息显示系统重现的结果。

图2-17　原始图像

图2-18　全息图

图2-19　由全息图用计算机模拟重构图像

图2-20　全息显示系统重构的图