22013-2016级(A类、工科数分)试卷

2013级（下）（A 类、工科数分）期中试卷

一、填空题

1．设f（x，y）＝y2e2x＋（x－1）arctan，则fy（1，1）＝_________．

2．设z＝xexy，则x＝_________．

3．曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程是_________．

4．｜x－y｜dy＝________．

5．（A 类高数题）设z＝x2－xy＋y2在点（1，1）处沿方向a的方向导数取到最大值，且｜a｜＝1，则a＝________．

6．（工科数分题）设其中u∈（0，π），v∈（－∞，＋∞），则

7．复数（1＋i）i的主值是_________．

二、单项选择题

8．（A 类高数题）设函数f（u）连续，则＝（　）

9．（工科数分题）下列命题中正确的是（　）

（A）若＝a，则f（x，y）在点（x0，y0）处连续

（B）在点（x0，y0）处连续

（C）若f（x，y）存在fx（x0，y0），fy（x0，y0），则f（x，y）在点（x0，y0）处可微

（D）若f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处连续

10．设Ω＝｛（x，y，z）｜x2＋y2＋z2≤1｝，Ω1为Ω在第一卦限的部分，则下列等式成立的是（　）

11．设C为曲线x＝etcost，y＝etsint，z＝et上对应于t从0变到2的一段弧，则曲线积分＝（　）

12．设Ω＝｛（x，y，z）｜x2＋y2＋z2≤1｝，则三重积分＝（　）

三、计算下列各题

13．设z＝，其中f 具有二阶连续偏导数，计算

14．计算二次积分

15．求函数f（x，y）＝x3－y3－3x2＋3y－9x 的极值．

16．设上半球面Σ＝｛（x，y，z）｜z＝面密度为常数μ，求Σ 的质心坐标．

17．已知函数u＝f（x，y，z，t）关于各变量都具有一阶连续偏导数，其中函数z＝z（y）和t＝t（y）由方程组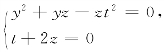确定，求

四、综合题

18．设f（z）＝u（x，y）＋iv（x，y）是解析函数，其中实部u（x，y）＝e－ycosx＋xy，求虚部v（x，y），并求f（z）的表达式．（自变量单独用z表示）

19．计算三次积分

20．设函数f（u）满足：f（0）＝0，f′（0）＝1，Ω＝｛（x，y，z）｜x2＋y2＋z2≤2tz｝，计算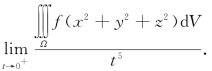

2014级（下）（A 类、工科数分）期中试卷

一、填空题

1．曲线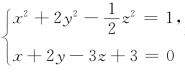在点（1，1，2）处的切线方程是_________．

2．设ez－1＋＝0，则z的主值是_________．

3．设z＝z（x，y）是由方程du＋sin（x－2y）＝0所确定的隐函数，则在点（0，0）处的全微分＝_________．

4．设平面曲线C 为圆周x2＋y2＝1，则曲线积分＝_________．

5．交换积分次序＝________．

二、单项选择题

6．已知曲面2z＝x2＋y2在点M 处的切面平行于平面x－y＋z＝1，则点M的坐标为（　）

（A）（－1，1，1）　（B）（－1，－1，1）　（C）（1，－1，1）　（D）（1，1，1）

7．设f（z）为复变函数，下列命题正确的是（　）

（A）如果z0是f（z）的奇点，则f（z）在z0处必不可导

（B）如果f（z）在z0处可导，则f（z）在z0处解析

（C）如果f（z）的实部u（x，y）与虚部v（x，y）在区域D 内满足条件ux＝vy，uy＝－vx，则f（x）在区域D 内解析

（D）如果f（z）在区域D 内可导，则f（z）在区域D 内解析

8．设函数f（x）具有二阶连续导数，且f（x）＞0，f′（0）＝0，则函数z＝f（x）lnf（y）在点（0，0）处取得极小值的一个充分条件是（　）

（A）f（0）＞0，f″（0）＞0　（B）f（0）＞1，f″（0）＜0

（C）f（0）＜1，f″（0）＞0　（D）f（0）＜1，f″（0）＜0

9．若I1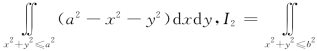＝（a2－x2－y2）dxdy，其中常数a，b都大于零，则（　）

（A）I1≤I2　（B）I1≥I2

（C）当a＜b时，I1＜I2　（D）当a＞b时，I1＜I2

三、计算下列各题

10．设z＝＋g（xy），其中f具有二阶连续偏导数，g具有二阶导数，计算

11．计算函数u＝在点M（1，－1，1）处沿曲面2z＝x2＋y2在点M 处的外法线方向n 的方向导数

12．设f（z）＝u（x，y）＋iv（x，y）为解析函数，其中v（x，y）＝4xy（x2－y2），试求f（z）的表达式，满足f（0）＝1．（自变量单独用z表示）

13．计算积分

14．计算三重积分

其中Ω是由平面x＝0，y＝0，z＝0与x＋y＋z＝1围成的四面体．

四、综合题

15．（A类高数题）已知球体Ω：x2＋y2＋z2≤R2内任一点处的密度与该点到点P0（0，0，R）的距离的平方成正比（比例系数k＞0），试求球体Ω的质心坐标．

16．（工科数分题）设f（x，y）＝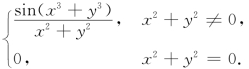

（1）计算f（x，y）在点（0，0）处的两个偏导数fx（0，0），fy（0，0）；

（2）判断f（x，y）在点（0，0）处是否可微，并证明你的结论．

17．计算圆柱面x2＋y2＝ay（a＞0）介于平面z＝0与曲面z＝（h＞0）之间部分的面积．

18．已知圆（x－1）2＋y2＝1内切于椭圆＝1（a＞0，b＞0，a≠b）．

（1）证明：a2－a2b2＋b4＝0；

（2）求上述椭圆所围区域的面积达到最小时的椭圆方程．

2015级（下）（A 类、工科数分）期中试卷

一、填空题

1．曲面2z－ez＋2xy＝3在点（1，2，0）处的切平面方程为________．

2．函数u＝2xy－z2在点（2，－1，1）处方向导数的最大值为_________．

3．设z＝arctan（xy），则dz＝_________．

4．设ez＋1－i＝0，则z＝________．

5．交换积分次序＝________．

6．设曲线C：x2＋y2＝4（y≥0），则曲线积分＝_________．

7．（A 类高数题）由方程x＋y＋z＝ez确定的隐函数z＝z（x，y）在x＝e，y＝－1，z＝1处的二阶偏导数＝________．

8．（工科数分题）设z＝z（x，y）是由方程x＋y＋z＝ez确定的隐函数，则＝_________．

9．（工科数分题）设区域＝________．

10．设 柱 面＝________．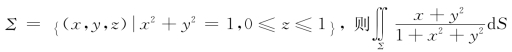

二、计算下列各题

11．设z＝f（x，x－2y，xy），其中f 具有二阶连续偏导数，求

12．计算二次积分

13．求曲线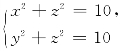在点M（1，1，3）处的切线方程．

14．已知解析函数f（z）的实部u（x，y）＝xy＋e－ycosx，求解析函数f（z）（自变量单独用z表示）和f′（i）．

15．计算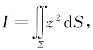其中Σ是锥面z＝被柱面x2＋y2＝2x所割下的有限部分．

三、综合题

16．若上半球体Ω：x2＋y2＋z2≤2z（z≥1）内各点处的密度等于该点到原点的距离的平方，试求Ω的质量．

17．（A 类高数题）求曲面z＝x2＋y2与平面x＋y－2z－2＝0的最短距离．

18．（工科数分题）设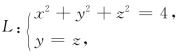其线密度μ＝1，求L 关于z 轴的转动惯量．

19．（工科数分题）设f（x，y）＝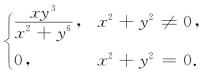

（1）f（x，y）在点（0，0）处沿任意方向的方向导数是否存在？在存在的方向上求f（x，y）在点（0，0）处沿该方向的方向导数．

（2）f（x，y）在点（0，0）处是否可微？并证明你的结论．

20．已知函数f（x，y）满足fxy（x，y）＝2（y＋1）ex，fx（x，0）＝（x＋1）ex，f（0，y）＝y2＋2y，求f（x，y）的极值．

2016级（下）（A 类、工科数分）期中试卷

一、填空题

1．设z＝＝_________．

2．设ez＝－3＋4i，则Rez＝_________，Imz＝_________．

3．设直线在平面Π 上，且平面Π 与曲面z＝x2＋y2相切于点（1，－2，5），则a＝________，b＝________．

4．二重积分cos2xdx＝_________．

5．将直角坐标系下的三次积分化为球面坐标系下的三次积分为__________________________________．

二、单项选择题

6．（A 类高数题）设＝0，则f（x，y）在点（0，0）处（　）

（A）不连续　（B）连续但是偏导数不存在

（C）偏导数存在但是不可微　（D）可微

7．（工科数分题）设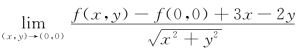＝0，则（　）

（A）df（0，0）＝0　（B）df（0，0）不存在

（C）df（0，0）＝3dx－2dy　（D）df（0，0）＝－3dx＋2dy

8．设f（x，y）与φ（x，y）均为可微函数，且φy（x，y）≠0．已经（x0，y0）是f（x，y）在约束条件φ（x，y）＝0下的一个极值点，下列选项正确的是（　）

（A）若fx（x0，y0）＝0，则fy（x0，y0）＝0

（B）若fx（x0，y0）＝0，则fy（x0，y0）≠0

（C）若fx（x0，y0）≠0，则fy（x0，y0）＝0

（D）若fx（x0，y0）≠0，则fy（x0，y0）≠0

9．函数f（x，y）＝1＋x＋y在区域上的最大值与最小值之积为（　）

10．设L 是以A（1，1），B（－1，1），C（－1，－1），D（1，－1）为顶点的正方形边界，则＝（　）

（A）0　（B）8　（C）4ln2　（D）8ln2

三、计算下列各题

11．（A 类高数题）求函数

在点处沿曲线＝1在该点的内法线方向的方向导数．

12．（工科数分题）设g（x，y）＝其中f（u，v）具有二阶连续偏导数，且满足＝1，求

13．设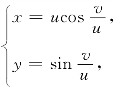求反函数组的偏导数ux，uy，vx，vy．

14．设f（x，y）在闭区域上连续，且

求f（x，y）．

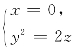15．求三重积分其中Ω是由曲线绕z 轴旋转而成的曲面与平面z＝2围成的立体．

16．设D 是由抛物线y＝x2及直线y＝1围成的平面薄片，薄片上点（x，y）的密度函数为μ（x，y）＝x＋1，求该薄片D 对直线y＝－1的转动惯量．

四、综合题

17．计算二重积分其中Σ 是柱面x2＋y2＝2ay（a>0）被锥面z＝和平面z＝2a所截下的部分．

18．求曲线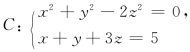上到xOy 平面的距离最远的点和最近的点．(www.xing528.com)

19．已知函数f（z）＝u＋iv的区域D 内解析，且在D 内是常数，证明：f（z）在D 内也是常数．

2013级（下）（A 类、工科数分）期末试卷

一、填空题

1．幂级数的收敛域为_________．

2．曲线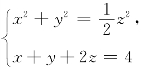在点（1，－1，2）处的切线方程为________．

3．设f（x，y）可微，且f（x，3x）＝x4，fy（1，3）＝，则fx（1，3）＝________．

4．向量场F＝2xyi－y2j＋xyzk在点（1，1，2）处的散度＝________．

5．若级数（a＞0，s＞0）收敛，则a和s满足的条件是_________．

6．已知dy是某函数的全微分，则a与b之间的关系是_________．

7．设f（x）∈C［0，π］，－∞＜x＜＋∞，其中bn＝sinnxdx（n＝1，2，…），则＝_________．

8．设C：｜z｜＝3，取逆时针方向，则＝_________．

9．留数＝________．

二、计算下列各题

10．计算积分

11．计算二重积分其中D＝｛（x，y）｜x2＋y2≤x＋2y＋1｝．

12．计算第二型曲面积分

其中Σ 为曲面z＝2－x2－y2（1≤z≤2）的上侧．

13．求幂级数的收敛半径与收敛域．

14．设f（x）＝

三、综合题

15．计算第二型曲线积分

其中L 是曲线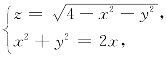从z轴的正向往负向看，L 为逆时针方向．

16．将函数f（x）＝展开为x－1的幂级数，并指明收敛域．

17．（A类高数题）设物体位于Ω＝｛（x，y，z）｜－1≤z≤1｝，其密度函数为ρ＝e｜z｜，求此物体的质量．

18．（工科数分题）证明：函数项级数在（－∞，＋∞）上非一致收敛，但在（－∞，＋∞）上内闭一致收敛．

19．求数项级数

的和．（其中（2n）！！＝2×4×6×…×（2n），0！！＝1）

2014级（下）（A 类、工科数分）期末试卷

一、填空题

1．设f（t）可导，且f′（e2）＝1，又u（x，y）＝f（xy），则＝_________．

2．若du＝（x2＋2xy3）dx＋（3x2y2＋cosy）dy，则u＝________．

3．已知幂函数在x＝5处条件收敛，则幂级数的收敛半径R＝________．

4．函数f（x，y）＝xy－y在闭区域D＝｛（x，y）｜x2＋y2≤1｝上的最大变化率（即方向导数的最大值）为_________．

5．复积分＝_________（积分路径取逆时针方向）．

6．留数＝_________．

7．正弦级数的和函数S（x）在（0，π）上的表达式为则S（x）在x＝π处的值＝_________．

8．当α＝_________，β＝_________时，向量场A＝（2x＋αy）i＋（x＋3z）j＋（βy－z）k为有势场．

9．若级数收敛，则a的取值范围是_________．

二、计算下列各题

10．判断级数的敛散性．

11．将函数f（x）＝ln（3＋2x＋x2）展开为x＋1的幂级数，并确定收敛域．

12．计算第二型曲面积分ydz∧dx＋（z＋1）dx∧dy，其中Σ是圆柱面x2＋y2＝4被平面x＋z＝2和z＝0所截下的部分，取外侧．

13．计算第二型曲线积分其中C是以A（－1，0）为起点，B（1，0）为终点的下半单位圆周y＝－

14．计算三重积分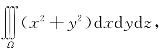其中Ω是由曲线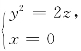绕z轴旋转而成的曲面，以及平面z＝2与平面z＝8所围成的区域．

三、综合题

15．计算第二型曲线积分其中L 是x2＋y2＝1与x＋y＋z＝1的交线，从x 轴的正向看是逆时针方向．

16．计算第一型曲面积分其中S是圆锥面z＝被圆柱面x2＋y2＝2ax（a＞0）所割下的部分．

17．（A 类高数题）求数项级数的和．

18．（工科数分题）证明：函数项级数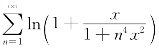关于x∈（－∞，＋∞）一致收敛．

19．判断级数是否收敛，如收敛，是绝对收敛还是条件收敛？并证明你的结论．

2015级（下）（A 类）期末试卷

一、填空题

1．函数f（x，y，z）＝xyz 在点（1，0，1）处沿曲线x＝t，y＝1－t2，z＝t3在该点指向x 轴负向一侧的切线方向的方向导数为_________．

2．设g（x）有连续导数，且g（0）＝0，g′（0）＝1，f（x，y）在点（0，0）的某邻域内连续，则＝________．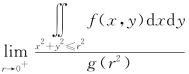

3．设Σ为球面x2＋y2＋z2＝R2，cosα，cosβ，cosγ为该球面外法线方向的方向余弦，则＝________．

4．已知级数在x>0时发散，在x＝0处收敛，则a＝_________．

5．幂级数的收敛域为_________．

6．设C 为椭圆＝1，取逆时针方向，则＝________．

7．复积分＝_________（积分路径取逆时针方向）．

8．留数＝_________．

9．设u＝xy2－z3，则A＝gradu＝_________，rotA＝_________．

二、计算下列各题

10．求由锥面z＝与平面z＝1－x 所围立体的表面积．

11．计算其中L为由点A（π，0）沿曲线y＝πcos到点B（0，π）的弧段．

12．求数项级数的和．

13．将函数f（x）＝arctan展开为x 的幂级数．

14．求幂级数的收敛域．

三、综合题

15．计算第二型曲线积分其中L 是曲线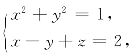从z轴正向往z 轴负向看取顺时针方向．

16．计算第二型曲面积分其中Σ 是曲面z＝x2＋y2上满足z≤2x 的部分，取下侧．

17．将函数f（z）＝在圆环域内展开为Laurent级数．

18．设在上半平面内，函数f（x，y）具有连续偏导数，且对任意的t＞0都有

f（tx，ty）＝t－2f（x，y）

证明：对D 内的任意分段光滑的有向简单闭曲线L，都有

2015级（下）（工科数分）期末试卷

一、填空题

1．二元函数z＝x3－y3－3x2＋3y－9x 的极小值点为_________．

2．设则二重积分＝________．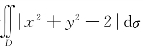

3．设曲线C：x2＋y2＝2x（y≥0），则曲线积分＝________．

4．幂级数的收敛域为________．

5．向量场A＝｛x2y，xy2，z2｝在点M（1，2，－1）处的散度为________．

6．若du＝（siny＋6xy2）dx＋（6x2y＋xcosy）dy，则u＝_________．

7．留数＝_________．

8．设C是正向圆周＝2，则积分＝_________．

9．函数f（x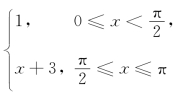）＝在［0，π］上展开为正弦级数，其和函数S（x）在x＝处的函数值＝_________．

二、计算下列各题

10．计算其中Ω为曲面x2＋y2＝16，y＋z＝4，z＝0所围成的闭区域．

11．求幂级数的和函数．

12．将函数f（x）＝ln（6＋x－x2）展开成x－1的幂级数．

13．将函数f（z）＝在圆环域内展成Laurent级数．

14．计算曲线积分其中L是沿曲线y＝πcos从A（π，0）到B（0，π）的一段．

三、综合题

15．计算曲线积分其中L 是曲线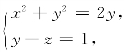其方向从z轴正向往z 轴负向看去为逆时针方向．

16．计算第二型曲面积分

其中Σ 为曲面z＝x2＋y2＋1（1≤z≤2），取下侧．

17．证明：函数项级数在区间［－2，2］上一致收敛．

18．（1）设un≥0，且级数u1－（u2＋u3＋u4）＋（u5＋u6＋u7＋u8＋u9）＋…收敛，试证：级数收敛；

（2）证明：级数收敛．

2016级（下）（A 类、工科数分）期末试卷

一、填空题

1．设则＝________．

2．与曲面x2＋y2＝4z 相切且与平面x ＋y ＋z＝1 平行的平面方程是________．

3．已知级数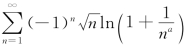条件收敛绝对收敛，则a的取值范围是________．

4．设C 为圆周｜z｜＝2，取逆时针方向，则＝________．

5．幂级数（x－1）n的收敛半径为_________．

6．设F（x，y，z）＝yi＋2xzj＋x2yk，则旋度＝________．

7．设f（x）＝ex2，则f（2n）（0）＝________．

8．设f（x）＝且以2为周期，S（x）为f（x）的Fourier级数的和函数，则S（3）＝_________．

9．使积分的值取到最大的正向分段光滑闭曲线L 的方程为_________________．

二、计算下列各题

10．设函数u＝u（x，y）由方程u＋eu＝2xy 确定，试求

11．判断级数的敛散性．

12．计算曲线积分其中L 是从点（1，1，1）到点（3，4，5）的直线段．

13．求函数f（z）＝的所有孤立奇点，并指出其类型，且求该函数在这些奇点处的留数．

14．把f（x）＝展开成x－1的幂级数，并指出其收敛域．

三、综合题

15．计算第二型曲面积分

其中，Σ 是曲面z＝1－x2－y2（z≥0）的上侧．

16．计算第二型曲线积分其中L 为由点A（2，0）沿曲线y＝到点B（0，2）的弧段．

17．（A 类高数题）求幂级数的收敛域与和函数，并求数项级数的和．

18．（工科数分题）设f（x）＝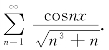

（1）证明：f（x）在（－∞，＋∞）上连续；

（2）记证明

19．设xn为方程xn＋xn－1＋…＋x－1＝0（n为大于1的整数）的唯一正实根，试判断级数的敛散性，并证明你的结论．