2013-2016级（上）试卷一

2013级（上）期中试卷

一、填空题

1．函数f（x）＝的间断点分别是_________和_________，它们分别是_________间断点和_________间断点．

2．已知f（x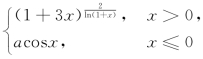）＝在x＝0处连续，则a＝________．

3．＝________．

4．设y＝arcsine2x，则微分dy＝_________．

5．当x→0时，ex－esinx与axn是等价无穷小，则n＝________，a＝________．

6．设f（x）＝x2ln（1＋x），则f（5）（0）＝________．

7．设y＝y（x）是由方程y＝－yex＋2eysinx－7x＋2所确定的隐函数，则y′（0）＝_________．

二、计算下列各题

8．（A、B高数题）求函数y＝的导数y′．

9．（工科数分题）用定义验证

10．计算极限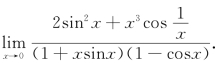

11．计算极限

12．讨论函数f（x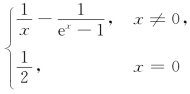）＝在x＝0处的连续性和可导性；若可导，求f′（0）．

三、综合题

13．已知曲线L 的参数方程为

（1）求曲线L 在t＝所对应的点处的切线方程；

（2）计算

14．（A、B高数题）试写出函数f（x）＝xsinx 带有Lagrange余项的4 阶Maclaurin公式．

15．（工科数分题）证明：函数f（x）＝在（－∞，＋∞）上一致连续．

16．（1）叙述Cauchy中值定理；

（2）证明Cauchy中值定理．

17．设

证明：数列｛xn｝收敛．

18．设f（x）在［a，b］上连续，在（a，b）内二阶可导，且f（a）f（b）＜0，f′（c）＝0，a＜c＜b，证明：当f（c）＜0时，存在ξ∈（a，b），使得f″（ξ）＞0．

2014级（上）期中试卷

一、填空题

1．函数y＝x5e－x的单调增加区间是_________．

2．设y＝logxe（x>0，x ≠1），则微分dy＝_________．

3．设f（x）在（－1，1）内连续，则＝_________．

4．函数f（x）＝的间断点是x＝________，是________间断点．

5．当x＝_________时，y＝arcsin的切线与y＝x2的切线互相垂直．

6．设数列｛an｝满足＝a（a为有限数），则＝________．

7．设y＝，则y（5）（x）＝________．

8．设f（x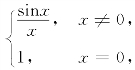）＝则f″（0）＝________．

二、计算下列各题

9．设函数f（x）＝ax＋xa＋xx＋aa（其中x＞0，x≠1；常数a＞0，a≠1），求f′（x）．

10．设y＝y（x）是由参数方程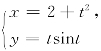所确定的函数，求

11．设方程y＝xln（x2＋y2）确定了一个二阶可导的隐函数y＝y（x），且y（1）＝0，求

12．求极限

三、综合题

13．设f（x）＝｜x2－4｜ln（3＋x）．

（1）讨论f（x）在其定义域内的可导性；

（2）在导数存在的点x 处，求f′（x）．

14．（A、B高数题）求f（x）＝arcsinx 带Peano余项的5阶Maclauris公式．

15．（工科数分题）用ε－X 语言验证

16．证明

17．（A、B高数题）设a1＝2，an＝2－（n＝2，3，…），证明数列｛an｝收敛，并求

18．（工科数分题）设对任意正整数n，有

yn＝｜x2－x1｜＋｜x3－x2｜＋…＋｜xn－xn－1｜≤C

其中C 为正常数．证明：

（1）数列｛yn｝收敛；

（2）数列｛xn｝收敛．

19．（1）证明方程xn＋nx－2＝0（n为正整数）存在唯一正实根an；

（2）计算

2015级（上）期中试卷

一、填空题

1．＝_________．

2．设f（x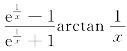）＝，则其间断点为_________，类型为_________．

3．设y＝xtanx，则dy＝_________．

4．（A、B高数题）由参数方程（t∈（0，＋∞））所确定的函数y＝y（x）在区间________内单调增加（填写最大的单调区间）．

5．（工科数分题）设f（x）在（0，＋∞）上一致连续，则＝________．

6．设f（x）＝tan2x＋cosx－1，则当x→0时，f（x）是x的________阶无穷小（填具体数字）．

二、单项选择题

7．设函数f（x）＝，则f（x）在（－∞，＋∞）内（　）

（A）处处可导　（B）恰有一个不可导点

（C）恰有两个不可导点　（D）至少有三个不可导点

8．设函数f（x）在x＝0连续，则下列命题错误的是（　）

（A）若存在，则f（0）＝0

（B）若存在，则f′（0）存在

（C）若存在，则f′（0）存在

（D）若存在，则f（0）＝0

9．下列说法正确的是（　）

（A）若函数y＝f（x）在定义区间I上连续，则f（x）在I上有界

（B）若函数y＝f（x）在x＝x0可导，则f（x）在x0的某邻域内连续

（C）若函数y＝f（x）在x＝x0二阶可导，则f（x）在x0的某邻域内一阶可导

（D）若函数y＝f（x）在（a，b）上可导，则f′（x）在（a，b）上连续

三、计算下列各题

10．求极限

11．已知＝c，求a，b，c．

12．（A、B高数题）求极限

13．设函数y＝y（x）由方程sin（xy）＋ln（y－x）＝x 所确定，求

14．设y＝x2cos（ax），其中a为非零常数，求y（10）（x）．

四、综合题

15．（工科数分题）用定义证明

16．（A、B高数题）设x1＞0，xn＋1＝（a＞1；n＝1，2，…），试利用单调有界原理证明数列｛xn｝收敛，并求其极限．

17．设f（x）＝（cosx－1），求f″（x）．

18．设f（x），g（x）在［a，b］上连续，在（a，b）内具有二阶导数且存在相等的最大值，若f（a）＝g（a），f（b）＝g（b），证明：存在ξ∈（a，b），使得f″（ξ）＝g″（ξ）．

19．（工科数分题）设xn＝，证明数列｛xn｝收敛．

2016级（上）（A 类、B类）期中试卷

一、填空题

1．极限＝_________．

2．设f（x）满足f（0）＝0，f′（0）＝1，则＝_________．

3．设函数由方程ln（x＋y＋e）＝ey所确定，则＝________．

4．设函数f（x）＝（ex－1）（e2x－2）…（enx－n），其中n为正整数，则f′（0）＝_________．

5．若x>0，则极限＝________．

二、选择题

6．设x→0时，函数f（x）＝3sinx－sin3x 与Cxk为等价无穷小量，则（　）

（A）k＝1，C＝4　（B）k＝1，C＝－4

（C）k＝3，C＝4　（D）k＝3，C＝－4

7．以下四个命题中，正确的是（　）

（A）若f（x）在（0，1）内连续，则f（x）在（0，1）内有界

（B）若f′（x）在（0，1）内连续，则f（x）在（0，1）内有界

（C）若可微函数f（x）在（0，1）内有界，则f′（x）在（0，1）内有界

（D）若f′（x）在（0，1）内有界，则f（x）在（0，1）内有界

8．函数f（x）＝的驻点的个数为（　）

（A）0个　（B）1个　（C）2个　（D）3个

9．设f（x）与g（x）在（－∞，＋∞）内有定义，分别各有唯一的间断点x1和x2，且x1≠x2，且必有间断点的函数为（　）

（A）f（g（x））　（B）f（x）＋g（x）

（C）f（x）g（x）　（D）f（sinx）＋g（cosx）

三、计算下列各题

10．求极限

11．设函数f（x）＝arctanx，且f（x）＝xf′（ξ），求极限

12．已知

13．设y＝f（sinx3）＋xx，其中函数f 二阶可导，求

14．已知f（x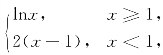）＝设g（x）＝f（f（x）），求g（x）及g′（x）．

四、综合题

15．讨论函数f（x）＝的连续性，并指出该函数的间断点的类型（需说明理由）．

16．已知数列｛an｝满足：

判断｛an｝是否收敛．若收敛，求其极限．

17．试写出函数y＝x2e2x在点x＝1处的带有Peano型余项的n阶Taylor公式．

18．设函数f（x）在［1，3］上连续，在（1，3）内可导，且f（1）＝1，f（2）＝5，f（3）＝2，证明：至少存在一点ξ∈（1，3），使得f′（ξ）＝2．

2016级（上）（工科数分）期中试卷

一、填空题

1．设f（x）＝（x－1）10sinx，则f（10）（1）＝________．

2．设f（x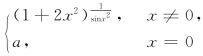）＝在x＝0处连续，则a＝_________．

3．设y＝xcos（1＋2x），则dy＝_________．

4．曲线y＝的渐近线方程为_________．(www.xing528.com)

5．设f′（0）＝1，f（0）＝0，则＝_________．

6．设＝2，则a＝_________，b＝_________．

7．设f（x）＝＝________．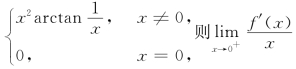

8．设函数f（x）＝有无穷间断点x＝0，有可去间断点x＝1，则a＝_________，b＝_________．

9．若x>0，则极限＝_________．

二、计算下列各题

10．设y＝y（x）是由参数方程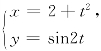所确定的函数，求

11．设y＝y（x）由方程y＝f（x－y）所确定，其中f 具有二阶导数，且其一阶导数不等于－1，求

12．设f（x）＝ln（1－x2），求f（n）（x）．

13．已知f（x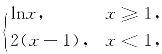）＝设g（x）＝f（f（x）），求g（x）及g′（x）．

14．已知f（x）＝，记a＝

（1）求a的值；

（2）若当x→0时，f（x）－a是xk的同阶无穷小，求k的值．

三、综合题

15．用定义证明

16．已知数列｛an｝满足：

判断｛an｝是否收敛．若收敛，求其极限．

17．证明：函数f（x）＝x＋cos2x 在（－∞，＋∞）上一致连续．

18．设函数f（x）在［1，3］上连续，在（1，3）内可导，且f（1）＝1，f（2）＝5，f（3）＝2，证明：至少存在一点ξ∈（1，3），使得f′（ξ）＝2．

2013级（上）期末试卷

一、填空题

1．＝________．

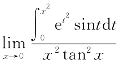2．设常数k＞0，则方程＋k＝0在（0，＋∞）内根的个数为_________．

3．曲线在点（x，y）＝处的切线方程是________．

4．设f（x）＝arcsin，则f′（x）的间断点是________，其类型为________．

5．若连续函数f（x）满足，则f（x）＝_________．

6．＝________．

7．（A、B高数题）曲线x2＋xy＋y2＝3在点（1，1）处的曲率κ＝_________．

8．（工科数分题）叙述函数f（x）在区间I上一致连续的定义：___________．

9．＝________．

10．微分方程ylnydx＋（x－lny）dy＝0的通解为_________．

二、计算下列各题

15．设f（x）在［0，＋∞）上连续，且f（x）＝2014，计算

三、综合题

16．（A、B高数题）设方程xy＋sin（πx）＋y＝0确定了x＝1附近的一个二阶可导的隐函数y＝y（x），求

17．（工科数分题）设xn＝1－＋…＋（－1）n－1，证明：数列｛xn｝收敛．

19．设f（x）为二阶可导函数，且满足

试求函数f（x）．

20．（1）求由曲线y＝x2，y＝sin围成的平面图形D 的面积；

（2）求（1）中的平面图形D 绕直线y＝1旋转而成的旋转体的体积．

2014级（上）期末试卷

一、填空题

1．由方程sin（x ＋y）＝y2cosx 确定的曲线L 在点（0，0）处的切线方程是________．

2．已知点（1，3）是曲线y＝ax3＋bx2的拐点，则a＝________，b＝________．

3．曲线y＝的渐近线方程是________．

4．＝________．

5．（A、B高数题）曲线x2＋xy＋y2＝3在点（1，1）处的曲率半径R＝________．

6．（工科数分题）用“ε－δ”语言表述f（x）＝A 的定义：________________．

7．极限的值是________．

8．设f（x）＝＝________．

9．连续函数f（x）满足f（x）－cos2x＝＝________．

10．已知y1＝x是微分方程（x2＋4）y″－2xy′＋2y＝0的一个解，则该方程的通解是y＝________．

二、计算下列各题

11．计算极限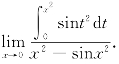

12．（A、B高数题）计算反常积分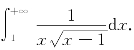

13．（工科数分题）判定反常积分dx 的敛散性．

14．计算不定积分

15．计算定积分

三、综合题

16．求初值问题＝1的解．

17．由椭圆＋y2＝1绕长轴旋转成一椭球体，沿其长轴方向穿心打一贯通的圆孔，使剩下部分的体积恰好等于椭球体体积的一半，试求该圆孔的半径R．

18．设f（x）＝min，求f（x）在区间［－5，3］上的最大值和最小值．

19．（A、B高数题）设f（x）为连续函数，且f（x）≤，证明：当x≥0时，f（x）≤0．

20．（工科数分题）证明：函数f（x）＝xarctanx 在（－∞，＋∞）上一致连续．

21．设f（x）在［a，b］上连续，在（a，b）内可导，且f′（x）单调递减，证明：

2015级（上）期末试卷

一、填空题

1．设f′（1）＝1，则＝_________．

2．当x→0时，x3－ln（1＋x2）dx 是x3的高阶无穷小，则a＝________．

3．（A、B高数题）曲线y＝e－x2（x>0）的拐点为________．

4．（工科数分题）已知反常积分收敛，则常数α的取值区间是________．

5．＝________．

6．设f（x）＝x（x2－1）（x2－2）（x3－3）＋4，则方程f′（x）＝0的正实根的个数为_________．

7．函数在区间［0，2］上的最大值为_________，最小值为_________．

8．＝_________．

9．若连续函数f（x）满足，则f（x）＝________．

10．（A、B高数题）设f（x）连续且满足方程则f（x）＝_________．

11．（工科数分题）叙述Cauchy 收敛准则：极限存在的充要条件是________．

二、计算下列各题

12．计算定积分

13．（A、B高数题）计算反常积分

14．（工科数分题）计算定积分

15．计算不定积分

16．计算定积分

17．由方程y＝2x2，y＝4所确定的抛物型薄片铅直地浸入水中，顶面与水面持平（长度单位为米）．

（1）试求薄片一侧所受到的水压力；

（2）如果此后水面以每分钟0．5m 的速度开始上涨，试计算薄片一侧所受水压力关于时间的变化率．

三、综合题

18．（A、B高数题）求微分方程y″＋4y＝x＋sin2x 的通解．

19．已知y1（x）＝ex，y2（x）＝u（x）ex是二阶微分方程

（2x－1）y″－（2x＋1）y′＋2y＝0

的两个解．若u（－1）＝e，u（0）＝－1，求u（x）并写出微分方程的通解．

20．设D 是由曲线

围成的平面区域，求D 的面积及D 绕x 轴旋转一周所成旋转体的体积．

21．证明：（1）（1＋x）ln2（1＋x）＜x2（x>－1且x ≠0）；

2016级（上）期末试卷

一、填空题

1．设f（x）＝（1－x2）（2－x2）…（2017－x2），则f′（－1）＝________．

2．曲线的拐点为_________．

3．设f（x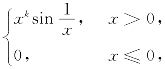）＝其导函数f′（x）在x＝0处连续，则k的取值区间为________．

4．＝_________．

5．（A、B高数题）椭圆在t＝对应的点处的曲率为________．

6．（A、B高数题）极限＝_________．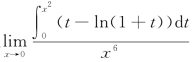

7．（工科数分题）设f（x）＝ex2，则f（6）（0）＝_________．

8．（工科数分题）函数f（x）＝在x＝2处带有Peano余项的二阶Taylor公式为_________．

9．函数f（x）＝lnx－＋1在区间（0，＋∞）内的零点个数为_________．

10．＝_________．

11．设f（x）满足＝cos3x＋C，则＝_________．

二、计算下列各题

12．计算不定积分

13．（A、B高数题）计算定积分

14．（工科数分题）计算积分

15．计算定积分，其中

16．（A、B高数题）计算反常积分

17．（工科数分题）计算极限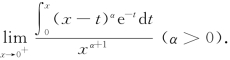

18．已知过（1，0）点的光滑曲线，其上任意点处的切线在y轴上的截距等于法线在x 轴上的截距，求该曲线方程．

三、综合题

19．设，其中f（x）连续，求f（x）．

20．（A、B高数题）计算曲线r＝asin3（0≤θ≤3π，a＞0）的弧长．

21．（工科数分题）讨论反常积分dx（p>0）的敛散性．

22．设曲线y＝e－x（x≥0）．

（1）将曲线y＝e－x，x轴，y轴和直线x＝t（t＞0）所围平面图形绕x轴旋转一周得一旋转体，求此旋转体体积V（t），并求满足V（a）＝的a；

（2）在曲线上求一点，使过该点的切线与两坐标轴所夹平面图形的面积最大，并求出该面积．

23．证明：（1）若t＞0，则lnt≤t－1；

（2）若f（x）在［0，1］上连续，且f（x）＞0，则

【注释】

[1]试卷中，A 为电类专业试题，B为非电类专业试题．