证明(x+y+z+)dA≥12πa^3(a>0)

1．证明（x＋y＋z＋）dA≥12πa3（a＞0），其中Σ 是球面

x2＋y2＋z2－2ax－2ay－2az＋2a2＝0

分析　首先求x＋y＋z＋在球面Σ 上的最小值m，然后验证

证　在球面Σ 上有

所以

因为Σ 的方程是（x－a）2＋（y－a）2＋（z－a）2＝a2，所以Σ上到原点距离最近的点（x0，y0，z0）在直线x＝y＝z上．点（x0，y0，z0）也正是函数x2＋y2＋z2在Σ上的最小值点．由

解　得x0＝y0＝z0＝a（注：另一解x1＝y1＝z1＝a对应于最远点，舍去），于是

所以

注　本题也可用Lagrange乘数法直接求函数x＋y＋z＋在Σ 上的最小值来证明，也可利用重心公式来证明．事实上，原命题等价于证明

利用重心公式

显然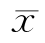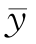（，，）＝（a，a，a），故结论成立．

2．设函数P（x，y），Q（x，y）在单连通区域D 上具有一阶连续偏导数，试证：若在D 内处处有，则曲线积分与路径无关，其中A，B 是D 内任意取定的两点．

证　如右图所示，任取两条以A为起点，B为终点且不相交的曲线C1，C2，则C1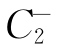＋构成正向的闭曲线，该闭曲线围成的区域为~D．则由Green公式得

即

故曲线积分Pdx＋Qdy 与路径无关．

3．已知曲线积分≡A，其中A 为常数，φ（x）有一阶连续导数，且φ（1）＝1，L 是围绕原点（0，0）一周的任一正向闭曲线．

（2）确定φ（x），并求A 的值．

分析　要证在任一不包含原点的单连通区域中曲线积分与路径无关，即证在单连通区域内任取两条具有相同起点和终点的曲线C1和C2，有

为了利用题中的条件，可以补上曲线C3，使C1＋C3和C2＋C3为围绕原点的闭曲线．然后再利用（1）的结论，得，从而求出φ（x）．

（1）证　如图，补上曲线C3，使C1＋C3，C2＋C3为围绕原点的正向闭曲线．由题意知

因而

即在任一不包含原点的单连通区域中，曲线积分与路径无关．

（2）解　由（1）知，当（x，y）≠（0，0）时，有

由此得xφ′（x）＝2φ（x），故φ（x）＝cx2．又φ（1）＝1，所以φ（x）＝x2．取积分路径L 为椭圆x2＋2y2＝1，正向，则其参数方程为

所以(www.xing528.com)

4．设f（x）为正值连续函数，试证不等式dx＋xf（y）dy≥2πa2，其中C 是圆周（x－a）2＋（y－a）2＝a2（a＞0），取逆时针方向．

分析　不等式的左端是一个第二型曲线积分，右端的值恰好是C 围成的圆域D 的面积的两倍，即故应考虑把第二型曲线积分转化为二重积分．

证　由Green公式得

其中D：（x－a）2＋（y－a）2≤a2．由轮换对称性得

所以

5．设函数u（x，y，z）具有连续的二阶偏导数，Σ是有界闭区域Ω的光滑边界曲面，记Δu＝，试证：

（1）是u（x，y，z）沿Σ的外法线方向的方向导数；

（2）若在Ω内Δu＝0，且函数u（x，y，z）在Σ 上取值为零，则在Ω内u ≡0．

分析　第（1）问中等式右边是第一型曲面积分，左边是三重积分，而Gauss公式是三重积分和第二型曲面积分的关系式，这些启示我们应先把第一型曲面积分化为第二型曲面积分，然后利用Gauss公式；对于第（2）问，由题意可以看出就是要证▽u＝0，利用求第（1）问的方法即可．

证　（1）设Σ 的外法线方向的方向余弦为｛cosα，cosβ，cosγ｝，则由方向导数的定义、第一型曲面积分和与第二型曲面积分的关系以及Gauss公式可得

（2）与第（1）问类似有

由题设知＝0，所以

从而在Ω内，有＝0，即ux＝uy＝uz＝0，故u为常数，又因为u在Σ 上取0，所以u≡0．

6．证明不等式：

其中C 是圆周x2＋y2＋x＋y＝0，取逆时针方向．

分析　利用Green公式把曲线积分化为二重积分来证．

证　记曲线C 所围成的区域为D，利用Green公式得

因为区域D 关于直线y＝x 对称，所以dxdy，代入上式得

又因为

所以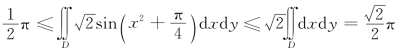，即

7．设曲线C：y＝sinx（x ∈［0，π］），证明

证　因为

得证．