圆锥体体积变化率及增减判断

1．已知圆锥体的体积V＝πR2H，若半径R以5cm／s的速度增加，而它的高H 以24cm／s的速率减小．

（1）求该圆锥体半径为30cm，高为70cm 时体积的变化率；

（2）这时圆锥体的体积是增大还是减小？

解　因为

所以

即此时圆锥体的体积变化率为－200πcm3／s，体积在减小．

2．设数量场u（x，y，z）＝x2＋2y2＋3z2＋xy＋3x－2y－6z，求：

（1）使梯度为零向量的点；

（2）在点（2，0，1）处沿哪一个方向的变化率最大，并求出最大变化率；

（3）使梯度垂直z轴的点．

解　gradu＝｛2x＋y＋3，4y＋x－2，6z－6｝．

（1）令gradu＝0，即有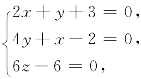解此方程组得x＝－2，y＝1，z＝1，即在点（－2，1，1）处梯度为零向量．

（2）变化率最大的方向为梯度方向．又

即在点（2，0，1）处沿x 轴正向变化率最大，最大变化率为7．

（3）由gradu·k＝6z－6＝0得z＝1，即在平面z＝1上梯度垂直于z轴．

3．设曲面S：2x2＋4y2＋z2＝4，平面Π：2x＋2y＋z＋5＝0，试求：

（1）曲面S 平行于平面Π 的切平面；

（2）曲面S 与平面Π 间的最短距离．

分析　本题第（1）问是曲面的切点待求的切平面问题，而S与Π的最短距离即为第（1）问中的切平面之一到Π 的距离．

解　（1）S 上任一点（x，y，z）处的法向量n＝｛2x，4y，z｝，依题意，n⊥Π，故

即x＝t，y＝，z＝t，代入曲面S 的方程，有

2t2＋t2＋t2＝4

解得t＝±1，于是切点为，相应的切平面方程为

Π1：2x＋2y＋z－4＝0　和　Π2：2x＋2y＋z＋4＝0

（2）Π1，Π2与平面Π 之间的距离分别为

由于曲面S 与Π 无交点，所以曲面S 与平面Π 的最短距离为

4．求曲线C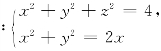在点M处的切线方程．

分析　曲线C 是由交面式方程给出的，其切线的求法一般有两种方法．

解法一　从几何观点来看，曲线C在点M 处的切线是曲面Σ1：x2＋y2＋z2＝4在点M 处的切平面与曲面Σ2：x2＋y2＝2x在点M 处的切平面的交线，因此只要将两切平面方程联立，就是切线方程．

曲面Σ1在点M处的法向量n1＝，曲面Σ2在点M（1，1，处的法向量n2＝｛0，2，0｝，相应的切平面分别为

于是切线方程为

解法二　从代数观点看，由方程组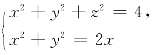确定隐函数y＝y（x），z＝z（x），于是曲线C的参数式方程可写为C：x＝x，y＝y（x），z＝z（x），其切线的方向向量a＝｛1，y′（x），z′（x）｝，其中y′（x），z′（x）可由方程组通过隐函数求导法得到，即

解得

于是曲线C 在点M处切线的方向向量a＝，故切线方程为

注　C 的方程也可用t作参数的方程表示，即

点M 对应参数t＝，此时切线的方向向量a＝｛x′（t），y′（t），z′（t）｝．

5．求曲线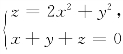的切线，使该切线平行于平面x＋y＝0．

分析　本题的关键是要在已知曲线上求一点，使该点的切向量与平面x＋y＝0 的法向量垂直．

解　首先可求出曲面z＝2x2＋y2在任一点（x，y，z）的法向量n1＝｛4x，2y，－1｝，再将n1与平面x＋y＋z＝0的法向量｛1，1，1｝作向量积，即得已知曲线上任一点的切向量

切向量s必与平面x＋y＝0的法向量｛1，1，0｝垂直，即2y－4x＝0，可化简为y－2x＝0．解方程组

得两组解（x，y，z）＝（0，0，0），（x，y，z）＝，分别得到满足题设条件的两条切线：

6．在xOy 平面上求一点M（x，y），使它到三条直线x＝0，y＝0，x－y＋1＝0的距离平方和为最小．

解　平面上任一点（x，y）到三条直线的距离平方和为

解方程组

得驻点x＝－．在整个xOy 平面上仅此一可能极值点M0，又(www.xing528.com)

则B2－AC＝1－9＜0，所以点是极小值点，从而必是最小值点．

7．在椭圆9x2＋16y2＝288上求一点P（a，b）（a＞0，b＞0），使过该点的切线与椭圆及两坐标轴围成的图形面积最小．

解　由于椭圆已定，因此只需求P 点的切线与坐标轴围成的三角形面积最小即可．令F（x，y）＝9x2＋16y2－288，则＝32b．于是过P 点的切线方程可写成

18a（x－a）＋32b（y－b）＝0

其截距式为

该切线与坐标轴围成的三角形面积为

求S 最小即求ab 最大．

令

G（a，b）＝ab＋λ（9a2＋16b2－288）　（a＞0，b＞0）

解方程组

得唯一驻点a＝4，b＝3，据问题的实际意义，点（4，3）即为所求．

8．求中心在原点的椭圆5x2＋4xy＋8y2＝1的长半轴与短半轴的长度．

解　设M（x，y）为椭圆上的任一点，点M 到原点的距离d＝，d的最大值即为长半轴a，最小值即为短半轴b．令

解方程组

由式（7．1．1）和（7．1．2）可得y＝2x或者y＝－x，再代入式（7．1．3）可得x2＋y2＝或者x2＋y2＝由于最值必存在，即得dmin＝，dmax＝．所以长半轴a＝，短半轴b＝

9．在椭圆上求一点P，使该点到原点的距离的平方为最大，并求出最大值．

解　这是一个条件极值问题．用Lagrange乘数法，令

L（x，y，z，λ1，λ2）＝x2＋y2＋z2＋λ1（x＋y＋z－4）＋λ2（x2＋y2－z）

解联立方程

求得两个点M1（1，1，2），M2（－2，－2，8），则有

由问题的实际意义可知距离平方的最大值存在，所以点M2（－2，－2，8）为最大值点，最大值为72．

10．在第一卦限内作曲面S：z＝4－－y2的切平面，使得切平面与三个坐标平面及曲面S 所围成的立体的体积最小，求切点的坐标，并求出最小体积．

解　设切点坐标为（a，b，c），由题设可知a，b，c皆大于0，过点（a，b，c）的切平面方程为

该平面与三个坐标平面所围成的四面体的体积

由Va＝0，Vb＝0，得a＝2，b＝1，这是唯一的极值点．再由问题的实际意义知a＝2，b＝1是问题的最小值点，因此所求最小体积为

11．试用两种方法（极值方法和非极值方法）求椭球面x2＋2y2＋4z2＝1与平面x＋y＋z＝之间的最短距离．

解法一（极值方法）　设M（x，y，z）为椭球面上任一点，则M 到已知平面的距离

令

解方程组

可得两个点

于是距离d1＝，故最短距离为d1＝

解法二（几何方法）　当椭球面上点M 处的切平面与已知平面平行时，其中的一个切点与平面的距离即为所求的最短距离．

椭球面上任一点M（x，y，z）处的法向量n＝｛2x，4y，8z｝，设过点M 的切平面平行于已知平面，则

即x＝，将它们代入椭球面方程，得

解得t＝±，故切点为，从而dmin＝

12．已知两平面光滑曲线f（x，y）＝0，g（x，y）＝0，又（α，β）和（ξ，η）分别为两曲线上的点，试证：若这两点是两曲线上相距最近的点，则必有

解法一（几何方法）　记Γ1：f（x，y）＝0，Γ2：g（x，y）＝0，又A（α，β），B（ξ，η）分别在Γ1，Γ2上，根据与Γ2上B 点处的切线垂直，则

即

同理可得

解法二（极值方法）　设（x1，y1），（x2，y2）分别是曲线f（x，y）＝0和g（x，y）＝0上的任意一点，而问题是要求函数s2＝（x1－x2）2＋（y1－y2）2在约束条件f（x1，y1）＝0，g（x2，y2）＝0下的条件极值点（α，β）和（ξ，η）必满足式（7．1．4）．作Lagrange函数

L（x1，x2，y1，y2，λ1，λ2）＝（x1－x2）2＋（y1－y2）2＋λ1f（x1，y1）＋λ2g（x2，y2）

建立方程组

设（x1，y1）＝（α，β），（x2，y2）＝（ξ，η）满足上述方程组，则有