高等数学试题分析(2017)

1．函数u（x，y）＝的不连续点集为_________．

解　应填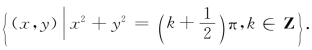

2．设f（x，y）＝则fx（0，0）＝________．

解　由定义，可得fx（0，0）＝＝1．

3．设z＝（x2＋y2），且Δx＝Δy＝0．1，则＝________．

解　因为＝fx（1，0）Δx＋fy（1，0）Δy，又

故＝0．1．

4．已知z＝z（x，y）是由方程zexz＋cos（yz）＝2所确定的隐函数，则dz＝________．

解　本题考查隐函数求全微分的方法．由于

exz（（xz＋1）dz＋z2dx）－sin（yz）（zdy＋ydz）＝0

于是

5．设u＝，则＝_________．

解　u关于变量x，y 求全微分，再将x＝1，y＝代入其中，即得

6．由方程xyz＋所确定的隐函数z＝z（x，y）在点（1，0，－1）处的全微分dz＝_________．

解　方程两边求微分后再将点（1，0，－1）的坐标代入即得dz＝dx－

7．设z＝z（x，y）由方程φ（x－2z，3y＋z）＝0确定，其中φ可微，则＝________．

分析　只需弄清楚隐函数中的函数关系，运用复合函数的求导法则即可，不必死记硬背隐函数求偏导数的公式．

解　等式φ（x－2z，3y＋z）＝0两边对x求偏导，得

解出

8．设z＝z（x，y）由方程φ（2z－3y，3x－4z，4y－2x）＝0确定，其中φ具有连续偏导数，则4＝_________．

解　求出后代入，应填3．

9．设函数y＝y（x）由方程f（xy，x2－y2）＝0确定，其中f（u，v）具有连续偏导数，则＝_________．

解　等式f（xy，x2－y2）＝0两边对x求导数，得

解出

10．设z＝z（x，y）是由方程

2sin（x＋2y－3z）＝x＋2y－3z

所确定的隐函数，则＝________．

解　因为

2cos（x＋2y－3z）·（dx＋2dy－3dz）＝dx＋2dy－3dz

于是＝1．

11．设z＝xy＋yx，则＝_________．

解　因为＝yxlny＋yxy－1，从而

12．设z＝z（x，y）由方程z＝f（t）dt确定，其中f连续，则dz＝________．

解　因为dz＝f（z）dz－f（xy）（ydx＋xdy），所以

13．若du＝（x4＋4xy3）dx＋（6x2y2－5y4）dy，则u＝________．

解　采用分组凑微分的办法，因为

于是

14．设f（x，y）＝x3y＋exy－sin（x2－y2），则fx（1，1）＝________．(https://www.xing528.com)

解　因为fx（x，y）＝3x2y＋yexy－2xcos（x2－y2），所以

fx（1，1）＝3＋e－2＝1＋e

15．已知（axsiny＋bx2y）dx＋（x3＋x2cosy）dy为某函数u（x，y）的全微分，则a＝________，b＝________．

解　采用分组凑微分的方法，因为

经观察，可得a＝2，b＝3．

16．函数u＝ln（xy＋y2ez）在点M（1，1，0）处的梯度＝________．

解　由梯度的定义可得

17．函数u＝x2yz在点M0（1，1，1）处沿方向l＝｛2，－2，1｝的方向导数＝_________．

解　函数u＝x2yz 在点M0（1，1，1）处的梯度为＝｛2，1，1｝，于是

18．函数u＝ln在点A（1，0，1）处沿着A 指向B（3，－2，2）的方向导数为________．

解　令＝l＝｛2，－2，1｝，则l°＝，又

故

19．函数u＝ln在点（3，4，1）处的方向导数的最大值是________．

解　函数u＝ln在点（3，4，1）处的梯度为，其模为，即为方向导数的最大值．

20．曲线，在t＝1 处的切线方程为_________．

解　切点为（1，－2，1），切线的方向向量

故切线方程为

21．曲线C（｜x｜≥1）上点________处的切线平行于平面x＋2y＋z＝4．

解　由题设知，应在曲线C上求一点，使该点处的切线的方向向量与已知平面的法向量｛1，2，1｝垂直．而方向向量为｛x′（t），y′（t），z′（t）｝＝｛1，2t，3t2｝，故有

｛1，2t，3t2｝·｛1，2，1｝＝1＋4t＋3t2＝（3t＋1）（t＋1）＝0

对于t＝－，由于不满足条件｜x｜≥1，故舍去．取t＝－1，则得

（x，y，z）＝（－1，1，－1）

22．曲面z＝x2＋y2在点（1，1，2）处指向下侧的单位法向量为________．

解　令F（x，y，z）＝z－x2－y2，曲面在点（1，1，2）处的法向量

因为指向下侧，所以cosγ＜0，故取n＝｛2，2，－1｝，单位化后得n°＝｛2，2，－1｝．

23．曲面xy＋yz＋zx－1＝0与平面x－3y＋z－4＝0在点M（1，－2，－3）处的法向量的交角为________或________．

解　平面的法向量n1＝｛1，－3，1｝，而曲面的法向量

因为n1·n2＝0，所以n1⊥n2，故交角为

24．曲面2xy－z－3ez＝1在点（1，2，0）处的法线方程为_________．

解　因为2ydx＋2xdy－（1＋3ez）dz＝0，代入（1，2，0）得

4dx＋2dy－4dz＝0

故法线方程为

25．曲面x2y＋ln（1＋z）－cosz＝1在点（1，2，0）处的切平面方程为________．

解　曲面x2y＋ln（1＋z）－cosz＝1在点（1，2，0）处的法向量为（4，1，1），于是所求的切平面方程为4x＋y＋z－6＝0．

26．设u＝f（r）连续可导，r＝，f′（0）＝2，则

解　因为

故