1．求过点M0（－1，－4，3）且与两直线
垂直的直线方程．
分析 已知M0，只要求出所求直线L 的方向向量即可．
解 直线L1的方向向量为
s1＝｛2，－4，1｝×｛1，3，0｝＝｛－3，1，10｝
L2的方向向量为s2＝｛4，－1，2｝，则L的方向向量s＝s1×s2＝｛12，46，－1｝，故L 的方程为
2．已知三角形的顶点A（4，0，0），B（0，－12，0），C（0，0，3），求BC 边上高线的方程．
分析 过A 作平面Π 垂直于
，则Π 与△ABC 所在平面Π1联立即为高线方程．
解 因为
＝｛0，12，3｝，则过点A 以
为法向量的平面为
Π：0（x－4）＋12（y－0）＋3（z－0）＝0， 即 4y＋z＝0
又△ABC 所在平面法向量n1＝
＝｛36，－12，48｝，得平面
Π1：36（x－4）－12（y－0）＋48（z－0）＝0
即3x－y＋4z－12＝0，故所求高线方程为
3．已知直线L 过点A（2，3，1），平行于Π1：3x＋2y－z＋6＝0且垂直于
试求L 的方程．
解 设直线L 的方向向量为s＝｛l，m，n｝，则由L ∥Π1得
3l＋2m－n＝0 （6．1．1）
又设L1的方向向量为s1，则s1＝｛2，－1，0｝×｛0，1，－4｝＝｛4，8，2｝，由L ⊥L1得
2l＋4m＋n＝0 （6．1．2）
由式（6．1．1）和式（6．1．2）联立得l＝－
m，n＝－
m，故
4．已知直线L：
，求：
（1）L 在平面z＝1上的投影L1的方程；
（2）点M（1，2，1）到L1的距离．
分析 平面z＝1与xOy 坐标面平行，故L 在z＝0上的投影柱面即为L 在平面z＝1上的投影柱面．又因点M 在z＝1上，故M 到L1的距离为xOy 平面上点（1，2）到L 在xOy 面上的投影直线的距离．
解 （1）将L化为一般式方程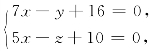
消去z得在xOy面上投影柱面方程为7x－y＋16＝0，故L1：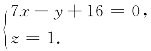
（2）M 到L1的距离，也就相当于xOy 面上点（1，2）到xOy 面上直线7x－y＋16＝0的距离，于是d＝
．（也可以用空间点M（1，2，1）到L1的距离公式求解）
5．求过直线L：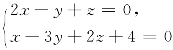
且平行于x 轴的平面方程．
分析 将平行x轴的平面方程法向量设为n＝｛0，B，C｝，再利用过直线L 可定出B 和C．
解 设所求平面的法向量为n＝｛0，B，C｝，直线L的方向向量为s＝｛1，－3，－5｝，由n⊥s，即n·s＝0，得3B＋5C＝0．所以
又因点
∈L，故所求平面方程为5y－3z－8＝0．
注 本题也可用平面束来作，不妨一试．
6．一平面过直线L1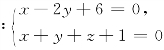
且与直线L2
之间的夹角为
，求该平面方程．
分析 利用平面束方程求解．
解 设过L1的平面束为Π：x－2y＋6＋λ（x＋y＋z＋1）＝0，即
（1＋λ）x＋（λ－2）y＋λz＋λ＋6＝0
记n＝｛1＋λ，λ－2，λ｝，L2的方向向量s2＝｛1，1，2｝，则
化简得23λ2－10λ－13＝0，解得λ＝1或λ＝－
，故
Π：2x－y＋z＋7＝0 或 Π：10x－59y－13z＋125＝0
7．求过点M（－1，2，－3），与已知直线L1：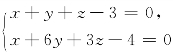
相交且与已知平面Π：6x－2y－3z＋10＝0平行的直线方程．
分析 若能求出所求直线的方向向量，直线方程即可求得．根据题设条件，可以较方便地求得所求直线与已知直线L1的交点，从而得到所求直线的方向向量．
解 设所求直线与L1的交点为（x0，y0，z0），则向量｛x0＋1，y0－2，z0＋3｝即为所求直线的方向向量，它必与平面Π 的法向量｛6，－2，－3｝垂直．于是可得以下线性方程组
解这个方程组，得x0＝1，y0＝－1，z0＝3，方向向量可取为｛2，－3，6｝，故所求直线方程为
8．求过点M（1，2，5）且与直线L1
相交并和向量j＝｛0，1，0｝成45°角的直线L 的方程．
解 在直线L1上取一点N（1，1，5），作向量
＝｛0，1，0｝，L1的方向向量τ＝｛2，3，2｝，再设直线L 的方向向量a＝｛l，m，n｝，由于L 与L1相交，因此以上三向量共面，所以有
即得l＝n．再由(www.xing528.com)
得到方程m2－l2－n2＝0，与l＝n联立，解得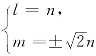
（n≠0），故可取a＝｛1，±
，1｝．所以求得直线L 的方程为
9．求过直线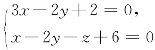
且与点（1，2，1）的距离为1的所有平面的方程．
解 设3x－2y＋2＋λ（x－2y－z＋6）＝0，则
即
6λ2＋14λ＋13＝4λ2＋4λ＋1
λ2＋5λ＋6＝0
得λ＝－2，λ＝－3，于是所求平面方程分别为
x＋2y＋2z－10＝0， 4y＋3z－16＝0
10．直线L：
绕z轴旋转一周，求该旋转曲面的方程．
解 直线L 的一般式方程为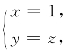
所以旋转曲面的方程为
x2＋y2＝1＋z2
11．求过点（0，2，4）且与两平面x＋2z＝1和y－3z＝2平行的直线方程．
解 所求直线的方向向量为
故所求直线的方程为
12．求直线L：
在平面Π：x－y＋2z－1＝0上的投影直线L0的方程，并求L0绕y 轴旋转一周所成曲面的方程．
解 设过直线L 的平面束方程为
x＋（λ－1）y＋λz－1－λ＝0
令该平面垂直于平面Π，则
1－λ＋1＋2λ＝0
得λ＝－2，即L0的方程为
对该方程组经整理得
因此旋转曲面方程为
13．求点（2，3，1）在直线
上的投影．
解 过点（2，3，1）且与直线
垂直的平面方程为
x－2＋2（y－3）＋3（z－1）＝0
即
x＋2y＋3z－11＝0
直线
与平面x＋2y＋3z－11＝0的交点即为所求的投影．
由
t－7＋2（2t－2）＋3（3t－2）－11＝0
解得t＝2，因此投影为（－5，2，4）．
14．求椭球面x2＋2y2＋3z2＝21上某点M 处的切平面，使其过直线
解 设M 点的坐标为（a，b，c），在该点处椭球面的法向量为（a，2b，3c），与直线的方向向量（2，1，－1）垂直，于是
2a＋2b－3c＝0
又由于点
在切平面上，于是
再由a2＋2b2＋3c2＝21，解得
a＝1， b＝2， c＝2 与 a＝3， b＝0， c＝2
故所求切平面方程分别为
x＋4y＋6z＝21， x＋2z＝7
15．求母线平行于直线x＝y＝z，准线为Γ：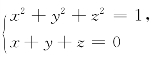
的柱面方程．
解 设M（x，y，z）是所求柱面上任一点，该点所在的母线与Γ 相交的点记为M1（a，b，c）．因为
∥v＝｛1，1，1｝，于是
又点M1在Γ 上，所以有
a2＋b2＋c2＝1， a＋b＋c＝0
消去a，b，c，得x2＋y2＋z2－xy－yz－zx＝
，即是所求柱面的方程．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
