高等数学试题分析(2017)中的单项选择题

1．设a，b，c均为非零向量，则与a不垂直的向量是（　）

（A）（a·c）b－（a·b）c　（B）b－

（C）a×b　（D）a＋（a×b）×a

解　因为a，b，c均为非零向量，不能排除a⊥b，a⊥c，所以排除（A）和（B）．又因为a⊥a×b，（C）不满足要求，故选（D）．

2．设向量α，β，γ满足（α＋2β－γ）·［（α－β）×（α－β－γ）］＝1，则以α，β，γ为棱的平行六面体的体积为（　）．

解：由混合积的几何意义知以α，β，γ为棱的平行六面体的体积为｜［α，β，γ］｜．依据数量积与向量积的运算规律化简上面的关系式可得3［α，β，γ］＝1，故V＝｜［α，β，γ］｜＝．因此正确答案为（C）．

3．设L1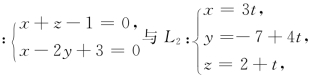则L1与L2（　）

（A）平行　（B）重合　（C）异面　（D）相交

解　两条直线的方向向量分别为s1＝｛2，1，－2｝，s2＝｛3，4，1｝，故s1与s2不平行，（A）和（B）不正确．取P1∈L1，P2（0，－7，2）∈L2，则≠0，故L1与L2异面，（C）正确．

4．设L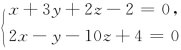：与Π：4x－2y＋z－2＝0，则（　）

（A）L ∥Π　（B）L 在Π 上　（C）L 与Π 斜交　（D）L ⊥Π

解　直线L 的方向向量为s＝｛1，3，2｝×｛2，－1，－10｝＝｛－28，14，－7｝，而平面Π 的法向量n＝｛4，－2，1｝，所以s∥n，即L ⊥Π，应选（D）．

5．方程y2－2x2－3z2＝0所确定的曲面是（　）

（A）椭球面　（B）双叶双曲面

（C）椭圆抛物面　（D）锥面

解　应选（D）．(www.xing528.com)

6．点（3，－1，2）关于平面2x－2y＋z－1＝0的对称点是（　）

（A）（0，4，0）　（B）（5，－3，3）　（C）（－1，3，0）　（D）（3，1，－2）

解　首先可以排除（A），（D）两个选项，因为这两个点与点（3，－1，2）的连线与平面2x－2y＋z－1＝0不垂直．又点（3，－1，2）到平面2x－2y＋z－1＝0的距离是3，根据这个要求，可知选（C）．

7．设直线L1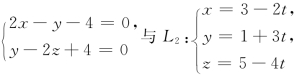：则L1与L2（　）

（A）垂直不相交　（B）垂直相交

（C）平行　（D）异面不垂直

解　L1的方向向量可取｛1，2，1｝，L2的方向向量可取｛－2，3，－4｝，这两个向量互相垂直，因此可排除（C）和（D）．再在直线L1上取一点A（2，0，2），在直线L2上取一点B（3，1，5），作向量＝｛1，1，3｝，L1的方向向量、L2的方向向量与向量作混合积，可知混合积不为零，因此L1与L2异面，故应选（A）．

8．两个非零向量a及b 的方向角分别为α，β，γ 及α′，β′，γ′，则cos（a，b）＝（　）

（A）cosαcosβcosγ＋cosα′cosβ′cosγ′

（B）cosαcosα′＋cosβcosβ′＋cosγcosγ′

（C）cos（α＋α′）＋cos（β＋β′）＋cos（γ＋γ′）

（D）cos（α－α′）＋cos（β－β′）＋cos（γ－γ′）

解　令a＝｛cosα，cosβ，cosγ｝，b＝｛cosα′，cosβ′，cosγ′｝，所以

故应选（B）．