练习题：高数试题分析中的级数收敛证明

1．讨论级数的敛散性．若收敛，是绝对收敛还是条件收敛？

2．讨论级数（a＞0）的敛散性．若收敛，是绝对收敛还是条件收敛？

3．判断级数是否收敛．若收敛，是条件收敛还是绝对收敛？

4．判别级数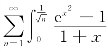dx 的敛散性，并说明理由．

5．讨论级数（q＞0）的敛散性．

6．讨论级数的敛散性，其中α为任意实数，β为正实数．

7．判别级数的敛散性，并说明理由．

8．判定级数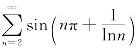是否绝对收敛、条件收敛或发散，并说明理由．

9．判定级数是否收敛．若收敛，是绝对收敛还是条件收敛？请说明理由．

10．求幂级数的和函数．

11．求幂级数（x－1）n的收敛域与和函数．

12．求的收敛域与和函数．

13．求幂级数的收敛域与和函数．

14．求幂级数的和函数，并指明收敛域．

15．求幂级数（－1）n－1nx2n的和函数，并指明收敛域．

16．求幂级数的收敛域与和函数．

17．求幂级数的和函数，并指明收敛域．

18．求幂级数的收敛域与和函数，并求的和．

19．求幂级数的收敛域及和函数，并求的和．

20．求幂级数的收敛域与和函数，并求数项级数的和．

21．求数项级数＋… 的和．

22．求幂级数的和函数，并求数项级数的和．

23．求数项级数的和．

24．讨论反常积分dx（p>0）的敛散性．

25．将函数f（x）＝展开为x－1的幂级数，并指明收敛域．

26．将函数f（x）＝展开为x＋1的幂级数．

27．将函数f（x）＝展开为x－2的幂级数．

28．将函数f（x）＝ln（2x2＋x－3）展开为x－3的幂级数，并求收敛域．

29．设f（x）＝，求f（n）（－1）．

30．求函数f（x）＝的Maclaurin展开式，并给出收敛域．

31．将函数f（x）＝展开为x－1的幂级数．

32．将函数f（x）＝展开为x的幂级数．

33．将函数f（x）＝ln（2x－x2）展开为x－1的幂级数，并指出其收敛域．

34．将函数f（x）＝ln展开为x的幂级数．(https://www.xing528.com)

35．将函数f（x）＝展开为x－1的幂级数，并写出收敛域．

36．求级数的收敛域．

37．将函数f（x）＝ln在x＝0处展开为Taylor级数，并确定收敛域．

38．将f（x）＝展开成周期为2π的Fourier级数，并求和函数S（x）在［－π，π］上的表达式．

39．设f（x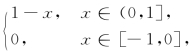）＝将f（x）在［－1，1］上展开为周期为2的Fourier级数，并求其和函数S（x）．

40．将函数f（x）＝1－｜x｜（｜x｜≤1）展开为以2为周期的Fourier级数．

41．将函数f（x）＝1－2x（0≤x≤1）展成周期为2的余弦级数．

42．将函数f（x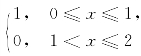）＝在［0，2］上展成正弦级数．

43．将函数f（x）＝（0≤x≤π）展成正弦级数．

44．将函数f（x）＝展开为余弦级数．

45．将函数f（x）＝1－x在［0，π］上展成余弦级数．

46．将函数

展开成正弦级数，并求级数的和．

47．设级数｜un－un－1｜收敛，且正项级数收敛，证明：级数收敛．

48．设＝1，如果级数收敛，问级数是否一定收敛？若判断一定收敛，请证明；若判断不一定收敛，请举例说明．

49．证明：级数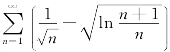收敛．

50．就x在区间上的不同取值，讨论级数的敛散性；当级数收敛时，判别其是绝对收敛还是条件收敛．

51．判别级数在x ∈（－∞，＋∞）的区间上是否一致收敛，并证明你的结论．

52．设有级数，证明：（1）该级数的收敛域为（1，＋∞）；（2）该级数的和函数在（1，＋∞）内连续．

53．证明：函数项级数的和函数S（x）在（1，＋∞）内连续．

54．设an≠0，n＝1，2，…，且＝a（a≠0），证明：级数｜an＋1－an｜与级数同时收敛或发散．

55．设a1＝1，a2＝2，当n≥3时，有an＝an－1＋an－2．

（1）证明不等式：0＜an－1＜an＜2an－1，n≥4；

（2）证明：级数收敛，且满足不等式2≤

56．已知fn（x）满足

f′n（x）＝fn（x）＋xn－1ex　（n为正整数）

且fn（1）＝，求函数项级数fn（x）的和函数．

57．设级数，其中常数a＞0，且a≠1，讨论当a满足什么条件时，该级数收敛；当a满足什么条件时，该级数发散．

58．设an＞0，bn＞0（n＝1，2，…），若存在常数α＞0，使得

证明：级数收敛．

59．设an＞0，且≥a1an＋1（n＝1，2，…），证明：级数收敛．

60．设f（x）＝，研究函数f（x）的定义域，并讨论其连续性．