证明题：正项级数的收敛性证明及递推关系分析

1．设两正数列｛an｝，｛bn｝满足条件bnan＋1≤bn＋1an（n＝1，2，…），试证明：

（1）若收敛，则也收敛；

（2）若发散，则也发散．

分析　在本题的证明过程中容易犯这样的错误：即认为正项级数收敛时，必有＝ρ＜1．事实上，比值判别法不能倒过来用，正项级数收敛时未必存在，即使极限存在，也未必小于1．我们采用下面两种方法来证明．

证法一　由bnan＋1≤bn＋1an（n＝1，2，…），可得．又因为

所以，（1）若收敛，则由比较判别法知收敛；（2）若发散，则由比较判别法知也发散，从而发散．

证法二　由bnan＋1≤bn＋1an，可得，从而正项数列单调减少且有下界，由单调有界原理知＝l存在，并且有0≤l＜＋∞．由比较判别法的极限形式知，当l＞0时，同敛散；当l＝0时，若发散，则也发散；且当l＝0时，若收敛，则收敛．综上即得所证．

2．设un＞0（n＝1，2，…），且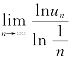＝A，试证明：当0＜A＜1时，级数发散；当A>1时，级数收敛．

分析　该命题也是正项级数的一个判敛法，称为对数判别法．证明的思路是用极限的定义导出n充分大后lnun与qln（q为某常数）之间的不等式关系，从而得un与之间的不等式关系，再用比较判别法．

证　因为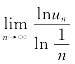＝A，所以任给ε＞0，存在正整数N，当n＞N时，有

当0＜A＜1时，取ε＞0，使A＋ε＝q＜1，于是lnun＞qln，即un＞（n＞N），而发散，所以发散；

当A>1时，取ε＞0，使A－ε＝p＞1，于是lnun＜pln，即un＜（n＞N），而收敛，所以收敛．

3．已知级数akxk＋1在区间［0，1］上收敛，其和函数为f（x），试证明：级数收敛．

证　f（x）＝akxk＋1，x∈［0，1］，由于级数ak收敛，所以ak＝0，因而｛ak｝有界．设｜ak｜≤M（k＝1，2，…），则

当n≥2时，有，又级数收敛，由比较判别法知原级数绝对收敛，故原级数收敛．

4．设｛un｝为单调增加的正数列，证明：若｛un｝有界，则级数收敛．

分析　本题证明思路是由所给条件去证明级数的部分和数列单调增加且上有界，从而级数收敛．

证　由正数列｛un｝单调增加，即知≥0．又｛un｝有界，即存在M>0，使得对任意正整数n，有0＜un≤M，则级数的部分和

于是｛Sn｝上方有界，由定义知级数收敛．

5．设正数列｛un｝单调减少，级数（－1）nun发散，证明：级数收敛．

证　因为un＞0，且｛un｝单调减少，所以存在．设其极限为A，则由极限的保号性知A≥0，但因为级数（－1）nun发散，故A>0．于是

由根值判别法知级数收敛．

6．设an＞0（n＝1，2，3，…），且＝λ>0，试证明：交错级数（－1）n－1an收敛．

证　因为＝λ＞0，所以存在N ∈N＊，当n＞N 时所以｛an｝单调减少．而发散，从而发散，所以lnan＝－∞，故an＝0．所以（－1）n－1an收敛．

7．若｛an｝为正数列，数列｛bn｝满足b1＝1，bn＋1＝bn＋（n＝1，2，…），试证：若级数an收敛，则数列｛bn｝也收敛．

分析　用比较判别法判别正项级数的敛散性，并利用级数收敛的定义将级数敛散性的判定与数列敛散性的判定联系起来．

证　根据递推关系bn＋1－bn＝＞0，有bn＋1≥bn（n＝1，2，…）．又b1＝1，所以bn≥1（n＝1，2，…）．于是由0＜bn＋1－bn≤an，级数an收敛，利用比较判别法知（bn＋1－bn）收敛，从而极限（bk＋1－bk）＝（bn＋1－b1）存在，即极限bn存在，也就是数列｛bn｝收敛．

8．证明：若an＞0，n≥1＋r（r＞0，n＝1，2，…），则收敛．

分析　正项级数的部分和数列有界是正项级数收敛的充分必要条件，利用这个充要条件和递推关系可证明本题．

证　由假设条件an＞0，n≥1＋r，可得

将上述一组不等式相加，可得

a1＋a2＋a3＋…＋an－nan＋1≥（1＋r）（a2＋a3＋…＋an＋1）

移项、整理得

记级数an的前n 项部分和为Sn，则Sn＜a1（n＝1，2，…），由正项级数收敛的充要条件可知级数an收敛．

9．设f（x）＝（0≤x≤1），则当0＜x＜1时，试证明

f（x）＋f（1－x）＋（lnx）ln（1－x）＝C　（C为常数）

并求C．

证　当0≤x≤1时，有

当0＜x＜1时，有(www.xing528.com)

所以xf′（x）＝－ln（1－x）＋C1，等式两边令x＝0，得C1＝0，所以

从而f′（1－x）＝－于是

根据Lagrange中值定理的推论知

f（x）＋f（1－x）＋（lnx）ln（1－x）＝C　（C为常数）

上式两边令x→0＋取极限得

其中极限（lnx）ln（1－x）可利用L'Hospital法则求得为0．

10．已知（1－x－x2）f（x）＝1，且an＝（n＝1，2，…），试证明：级数收敛．

分析　同学们可能会有如下想法：因f（x）＝，所以首先想直接求f（n）（0），从而得an再证，这实际上不可行；或者想将f（x）写成f（x）＝＋后展成幂级数，利用幂级数展开式的唯一性得an再证，这也比较复杂．

本题实际上不需知道f（n）（0），却可得到有关an＋2，an＋1，an之间的一个关系式．

证　设f（x）的Maclaurin展开式为f（x）＝，则由展开式的唯一性知

在该幂级数的收敛域内

于是得

a0＝1，a1＝1，an－an－1－an－2＝0或an＝an－1＋an－2　（n≥2）

由a0＝1，a1＝1及an＝an－1＋an－2（n≥2）易知｛an｝为正数列，且因为

an－an－1＝an－2＞0

所以｛an｝单调递增，故

an＝an－1＋an－2＜an－1＋an－1＝2an－1

从而an－1＞an，于是

an＝an－1＋an－2＞

故

由比较判别法可知收敛．

注　本题中的数列｛an｝称为Fibonacci数列．

11．证明：（1）级数在（－∞，＋∞）上一致收敛；

（2）存在ξ∈，使得

证　（1）因为，x∈（－∞，＋∞），而收敛，所以由M－判别法知在（－∞，＋∞）上一致收敛．

（2）令f（x）＝，则由（1）知f（x）在上连续．由于

而由比值判别法易知收敛，故由M－判别法知在（－∞，＋∞）内一致收敛，则f（x）在内 可 导，且f′（x）＝，由Lagrange中值定理知，存在ξ∈，使得

12．证明：函数项级数在［0，＋∞）上一致收敛．

分析　用M－判别法需求出优级数，而优级数不易看出时，采用求最大值的方法寻找优级数往往是有效的．

证　记un（x）＝x4e－nx，则

u′n（x）＝4x3e－nx－nx4e－nx＝e－nxx3（4－nx）

解得两个驻点x＝0，x＝，经判别x＝为最大值点，un（x）在［0，＋∞）上的最大值为，故

因为收敛，故由M－判别法知在［0，＋∞）上一致收敛．

13．试用Fourier级数证明：当0＜x＜π时，

证　设f（x）＝，0＜x＜π，将f（x）在（0，π）上展成正弦级数．为此先将f（x）作奇延拓，再作周期性延拓．由Euler－Fourier公式可得

an＝0　（n＝0，1，2，…）

于是由Dirichlet收敛定理得