高等数学试题分析(2017)：计算题分享

1．判别级数（－1）n－1的敛散性．

解　这是一个交错级数．显然

又因，所以

从而0＜un＜→0（n→∞），故由Leibniz判敛法知原级数收敛．

2．求常数a和b 的值，使级数［lnn＋aln（n＋1）＋bln（n＋2）］收敛．

分析　利用Taylor公式找出级数通项的同阶无穷小量，再利用比较判别法．

解　因为

令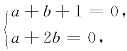得a＝－2，b＝1．当a＝－2，b＝1时，级数通项为

即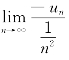＝1，而收敛，由比较判敛法知（－un）收敛，从而原级数收敛．

3．讨论级数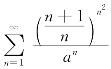（a＞0且a≠e）的敛散性．

解　由Cauchy根值判别法，因

当a＞e时，级数收敛；当a＜e时，级数发散．

4．就参数k的不同取值，讨论级数

的敛散性．

解　因为

所以

因此，由p级数的结论，可知当－k＞1，即k＜时，级数收敛；当k≥时，级数发散．

5．判断级数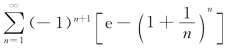是否收敛．若收敛，是绝对收敛还是条件收敛？

分析　本题需要用到数列单调增加收敛于e这一结果．

解　由于＜e，所以这是一个交错级数，且

所以由Leibniz判敛法知，原级数收敛．

再考查其绝对值级数，由于

而发散，故发散．

综上知，原级数条件收敛．

6．讨论级数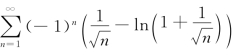的敛散性．若收敛，是绝对收敛还是条件收敛？

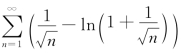解因此发散．又

令

因此f（x）单调增加，因而关于n 单调减少，由Leibniz判别法，知级数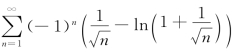收敛，于是该级数条件收敛．

7．试讨论级数（a＞0）的敛散性．若收敛，是绝对收敛还是条件收敛？

解　设un＝（－1）n，因为＝a，所以级数当0＜a＜1时收敛，当a＞1时发散．从而当0＜a＜1时绝对收敛，当a＞1时发散

当a＝1时，因为，而发散，所以发散．又因＝0，且，所以收敛．

综上知，当0＜a＜1时绝对收敛，当a＞1时发散，当a＝1时条件收敛．

8．判断级数的敛散性，其中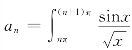dx．如果收敛，是条件收敛还是绝对收敛？

解　因为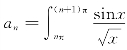dx，所以当n为偶数时，an＞0；n为奇数时，an＜0．故为交错级数．又

故｜an｜＝0．

又

故｜an｜单调递减．由Leibniz判别法得知收敛．

因为

所以发散，因此条件收敛．

9．求级数（x≥0，α为常数）的收敛域．

分析　这是一个讨论题，要根据常数α取值的不同，分别确定级数的收敛域．

解　当0≤x＜1时，对任何实数α，有0≤≤，可知级数收敛；当x＝1时，由于0＜＝，所以α＞1时级数收敛，α≤1时级数发散；当x>1时，因为，而由上可知，x>1时对任何实数α收敛，当α＞2时收敛，α≤2时发散，所以原级数在x>1时，当α＞2时收敛，α≤2时发散．

综上知，当α≤1时，收敛域为［0，1）；当1＜α≤2时，收敛域为［0，1］；当α＞2时，收敛域为［0，＋∞）．

10．求级数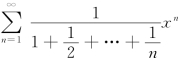的收敛域．

解　由于＝∞，又

因此收敛半径R＝1．

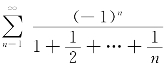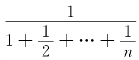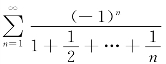当x＝－1时，级数变为，这是一交错级数，因为an＝单调减少，且an＝0，由Leibniz判别法知收敛．

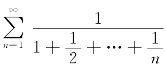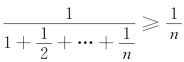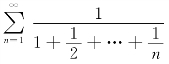当x＝1时，级数变为，an＝，而发散，因此发散．

因此，原级数的收敛域为［－1，1）．

11．设0≤an＜，则下列级数中，肯定收敛的是哪些级数？未必收敛的是哪些级数？对于肯定收敛的情形，请给出证明；对于未必收敛的情形，请举发散级数的例子，并予以证明．

解　（d）由于收敛，于是绝对收敛，当然收敛．

（a）未必收敛．例如an＝，级数发散．

（c）同样以an＝为例≥an，由比较判别法，得知发散．

（b）设an＝，则

因为收敛，而发散，所以（－1）nan发散．

12．求幂级数（b＞0）的收敛域．

解　收敛半径

当x＝±1时，原级数为若0＜b≤1，则因为≠0，所以原级数发散；若b＞1，则因为

故当n充分大时收敛，所以原级数绝对收敛．

综上，有

13．求数项级数的和．

解　我们已知

取x＝，得

14．求幂级数的收敛域与和函数．

分析　求收敛域的步骤同前；而求幂级数的和函数，往往是利用幂级数在收敛区间内可以逐项求导、逐项积分等性质，归为对某些已知其和函数的级数求和．

解　收敛半径

当x＝±时，原级数为（±1）n＋1·，由于收敛的必要条件不满足，此时级数发散，故该幂级数的收敛域为．其和函数

15．求级数的收敛域与和函数．(www.xing528.com)

分析　本题可通过变量替换，转化成幂级数求和函数的问题．

解　令y＝e－x，则，易求得幂级数的收敛域为（－1，1），即y＝e－x∈（－1，1），得原级数的收敛域为（0，＋∞）．

又和函数

16．求

分析　先求出幂级数的和函数，再求左极限．

解　易知级数的收敛域为（－1，1），记其和函数为S（x），则

所以

17．求数项级数的和．

分析　数项级数求和常常通过构造一个适当的幂级数来辅助完成．

解　构造幂级数n2xn－1，其收敛域为（－1，1）．记该幂级数的和函数为S（x），则数项级数的和为S

方法一　因为

所以，数项级数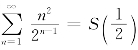＝12．

方法二　因为

所以＝12．

18．求级数的和．

解　构造幂级数，其收敛域为［－1，1］．记该幂级数的和函数为S（x），则S．因为

又S′（0）＝0，S（0）＝0，所以

19．求幂级数的收敛域与和函数S（x），并求的和．

解　收敛域为（－∞，＋∞）．又

所以

20．将函数f（x）＝展开成x＋1的幂级数．

分析　首先将函数f（x）分解为最简分式之和，再用间接法展开．

解　因为f（x）＝，且

所以

21．将函数f（x）＝展开成x－1的幂级数．

分析　f（x）＝，可考虑先将展开，再用逐项求导法得的展式．（另一方法：可由（1＋t）－2的展式，令t＝x－1而得）

解　因为

又幂级数在收敛区间内可以逐项求导，且收敛半径不变，所以

22．求f（x）＝的幂级数展开式，指出其收敛域．

解　由于

令g（x）＝，则

得g（x）＝（n＋1）xn，故

23．将f（x）＝展成x 的幂级数，并求f（100）（0）的值．

解　因为

两边对x 求二阶导数，得

所以

当n＝100时，可得

所以

f（100）（0）＝1012·100！

24．将函数f（x）＝arctanx－x 展开成x 的幂级数．

分析　若不加处理直接用间接法展开，一下子不容易得到结果．注意到f′（x）的表达式很简单，可先将f′（x）展成x的幂级数，再利用幂级数的性质去求得f（x）关于x 的幂级数展式．

解　因为

且f（0）＝0，所以

25．将函数f（x）＝ln（x2＋x－2）展开成x－2的幂级数．

解　因为

f（x）＝ln（x＋2）（x－1）＝ln（x＋2）＋ln（x－1）

而

所以

26．试求级数的和函数S（x），并求出S（x）在x＝1处的幂级数展开式．

27．将f（x）＝（0≤x≤π）展开成正弦级数．

解　根据题意得

所以

28．将f（x）＝1－x在［0，π］上展开成余弦级数．

解　将f（x）作偶延拓，再作周期性延拓．由Euler－Fourier公式得

由Dirichlet收敛定理，得

29．设f（x）＝

（1）试将f（x）在［0，2］上展成正弦级数；

（2）记此正弦级数的和函数为S（x），求S（1）和S

解　（1）将f（x）作奇延拓．由Euler－Fourier公式得

an＝0　（n＝0，1，2，…）

由Dirichlet收敛定理，得

30．将f（x）＝｜x｜，x∈［－1，1］展开的周期为2的Fourier级数．

解　f（x）为偶函数，因此

31．将函数f（x）＝展开成周期为4的Fourier级数，并写出该级数的和函数S（x）在区间［2，6］上的表达式．

解　由Euler－Fourier公式得

根据Dirichlet收敛定理，得

和函数S（x）在区间［2，6］上的表达式为