高等数学试题分析：单项选择题解答(2017)

1．已知级数（－1）n－1un＝2，u2n－1＝5，则级数un＝（　）

（A）3　（B）7　（C）8　（D）9

解　因为＝2×5－2＝8，故选（C）．

2．若是正项级数，则（　）

（A）若nan＝0，则收敛　（B）若＝λ≠0，则发散

（C）若收敛，则n2an＝0　（D）若发散，则＝λ≠0

解　（A）错误．反例：an＝＝0，但是发散．

（B）正确．因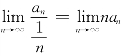＝λ≠0，发散，由比较判别法得发散．

（C）错误．反例：设an＝收敛，但是＝1≠0．

（D）错误．反例：设an＝发散，但是＝0．

3．下列结论正确的是（　）

（A）若级数（an＋bn）发散，则级数与都发散

（B）若的收敛半径为4，则的收敛半径为2

（C）若z＝f（x，y）在点M 处存在偏导数则z＝f（x，y）在点M 处连续

（D）级数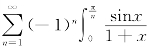dx 条件收敛

解　（A）错，用反证法很容易证明：若级数收敛，发散，则（an＋bn）必然发散．

（C）错，例如

经计算可得＝0，但极限f（x，y）不存在，因此z＝f（x，y）在点（0，0）处不连续．

（D）错，记an＝，则xdx＝，由此可知级数dx 绝对收敛．

应当选（B），若x2＝y，则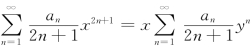，由题设知作为y的幂级数的收敛半径为4．即当＜2时，收敛，＞2时，发散，故收敛半径为2．

4．设有一任意项级数un，若｜un｜＞｜un＋1｜（n＝1，2，…），且＝0，则该级数（　）

（A）条件收敛　（B）绝对收敛

（C）发散　（D）可能收敛也可能发散

解　用排除法．例如，取｜un｜＝（n＝1，2，…），则是满足题设条件的绝对收敛级数，故（A）和（C）可排除；又如，取

则也满足题设条件，但不是绝对收敛级数，故（B）也排除．所以，应选（D）．

5．设un＞0（n＝1，2，…），如果＝l（0＜l＜＋∞），则交错项级数（－1）nun（　）

（A）绝对收敛　（B）条件收敛

（C）发散　（D）不能确定其敛散性

解　因为＝l（0＜l＜＋∞），而收敛，由比较判敛法知收敛，即（－1）nun绝对收敛．故选（A）．

6．设级数（－1）nan条件收敛，则必有（　）

（A）收敛　（B）收敛

（C）（an－an＋1）收敛　（D）都收敛

解　用排除法．例如，取an＝，则（－1）nan条件收敛，但均发散，故（A）和（B）可排除；又如，取an＝，则（－1）nan条件收敛，但发散，故（D）可排除．所以选（C）．或者由级数的性质：收敛级数加括号后得到的级数仍收敛，可直接知应选（C）．

7．若级数（－1）nnsin绝对收敛，则必有（　）

（A）p＞2　（B）p≥2　（C）1＜p＜2　（D）0＜p≤1

解　因为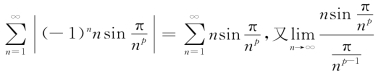＝1，故由比较判敛法知与同敛散，而收敛当且仅当p－1＞1，即p＞2，所以当p>2时，级数收敛，从而原级数绝对收敛．所以选（A）．

8．设常数k≠0，则级数（　）

（A）条件收敛　（B）绝对收敛

（C）发散　（D）敛散性与k的取值有关

解　因为记un＝，n＝1，2，…，则un～（n→∞），由于发散，所以原级数非绝对收敛．又当n≥2｜k｜时，un＝＝sin单调减少，且＝0，由Leibniz判敛法知原级数收敛．所以选（A）．

9．级数（α为实数）（　）

（A）条件收敛　（B）绝对收敛

（C）发散　（D）收敛性与α的取值有关

解　因为

所以an≠0，故原级数发散．所以选（C）．

10．设级数条件收敛，且＝ρ，则（　）

（A）ρ＝＋∞　（B）ρ＜1　（C）1＜ρ＜＋∞　（D）ρ＝1

解法一　如果ρ＜1，则级数绝对收敛，与题设条件收敛矛盾，所以排除（B）；如果1＜ρ≤＋∞，则级数一般项不趋于0，级数发散，也与题设矛盾，故（A）和（C）也排除．所以应选（D）．

解法二　考虑幂级数anxn，因其在x＝1条件收敛，所以由Abel定理知，级数anxn的收敛半径R＝1，所以ρ＝＝1．

11．幂级数an（x－1）n在x＝－2处收敛，则此级数在x＝3处（　）

（A）条件收敛　（B）绝对收敛

（C）发散　（D）不能确定其敛散性(https://www.xing528.com)

解　因为幂级数an（x－1）n在x＝－2处收敛，故由Abel定理知，至少对满足｜x－1｜＜｜－2－1｜＝3，即满足－2＜x＜4的点x，级数绝对收敛．故应选（B）．

12．设＝3，则级数的收敛半径（　）

（A）R＝3　（B）R＝　（C）R＝　（D）R＝

解　把该幂级数看成是一般的函数项级数un（x），其中

un（x）＝anx2n－1　（n＝1，2，…）

由于

故当3x2＜1即｜x｜＜时，级数绝对收敛；当3x2＞1即｜x｜＞时，级数发散．所以，该幂级数的收敛半径R＝．故应选（D）．

13．设＝2，则级数的收敛半径（　）

（A）R＝2　（B）R＝　（C）R＝　（D）R＝6

解　令y＝，则幂级数的收敛半径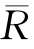＝．于是，当｜x＋3｜＝3｜y｜＜时，原幂级数绝对收敛；当｜x＋3｜＝3｜y｜＞时，原幂级数发散．所以，原幂级数的收敛半径R＝．故应选（C）．

14．下列函数项级数在给定的区间上不一致收敛的是（　）

解　当－∞＜x＜＋∞时，，而收敛．所以由M－判别法知，在（－∞，＋∞）上一致收敛；

当0≤x＜＋∞时，，而收敛，所以由M－判别法知，在［0，＋∞）上一致收敛；

当－∞＜x＜＋∞时，收敛，所以由M－判别法知，在（－∞，＋∞）上一致收敛．

用排除法，综上可知应选（C）（严格证明从略）．

15．下列反常积分中收敛的是（　）

解　本题考查用p 积分判定反常积分敛散性的方法．

由于当x→1－时，当x→∞时，当x→0＋时，因此（B），（C），（D）皆为错误的选项．下面分析选项（A）．由于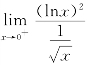＝0，而dx 收敛，于是（lnx）2dx 收敛，故选（A）．

16．下列反常积分中收敛的是（　）

解　先看（A）．当x→＋∞时，有

而dx 发散，所以dx 发散，即（A）是发散的积分．

再看（C）．0是瑕点．取xn＝，则

所以dx 发散．

再看（D）．1是瑕点，当x→1＋时，有

而发散，所以积分（D）是发散的．

最后看（B）．0不是瑕点．当x＞1时，因为0＜e－x2＜e－x，而e－xdx收敛，所以e－x2dx 收敛，故选（B）．

17．下列命题中正确的是（　）

（A）设an＞，则（－1）n－1an发散

（B）若＝r＞1，则｛un｝发散

（C）若条件收敛，绝对收敛，则（an＋bn）绝对收敛

（D）设α为常数，则级数的敛散性不能确定

解　先看（A）．取an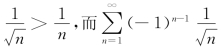＝收敛，所以（A）错．

再看（C）．若（an＋bn）绝对收敛，则令cn＝an＋bn，an＝cn－bn，立即可得an绝对收敛，矛盾．所以（C）错．

再看（D）．无论α等于多少，收敛，故绝对收敛．又发散，所以原级数发散，因此（D）错．

最后看（B）．由于＝r＞1，存在N，当n＞N 时，｜un＋1｜＞｜un｜．如果｛｜un｜｝有界，则极限｜un｜＝a（有限数），于是＝1，矛盾，所以｛un｝发散，故选（B）．

18．下列反常积分中收敛的是（　）

解　先看（A）．因为，而反常积分发散，因此发散，故不能选（A）．

再看（C）．根据p积分的敛散性的结论知收敛，而发散，因此发散，故不能选（C）．

再看（D）．1是瑕点，因为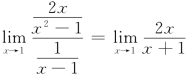＝1，由于p＝1，所以积分dx 发散，故不能选（D）．

最后看（B）．1是可能的瑕点，又

因此x＝1不是瑕点，所以选（B）．

19．设φ（x），ψ（x）在［－π，π］上连续，且φ（－x）＝ψ（x），则φ（x）的Fourier系数an，bn与ψ（x）的Fourier系数αn，βn 的关系是（　）

（A）an＝αn，bn＝βn　（B）an＝αn，bn＝－βn

（C）an＝－αn，bn＝βn　（D）an＝－αn，bn＝－βn

解　由Fourier系数的Euler－Fourier公式立即可知应选（B）．

20．设

其中

则S（2）＋S（－9）＝（　）

（A）－1　（B）1　（C）5　（D）7

解　题意是将定义在［0，4）上的函数f（x）奇延拓成［－4，4）上的函数F（x），再将F（x）以8为周期作周期延拓，将F（x）展开成Fourier级数，便将f（x）展开成正弦级数．由Dirichlet收敛定理，知

所以S（2）＋S（－9）＝－1．故应选（A）．