计算题解答及求导积分方法

1．已知f′（sin2x）＝cos2x＋tan2x（0＜x＜1），求f（x）．

分析　先求出f′（x）的表达式，积分可得f（x）．

解　考虑到cos2x＋tan2x＝1－2sin2x＋，于是

所以

2．计算

分析　这是有理函数的积分，通过拆项可将有理函数巧妙地化为部分分式和的形式．

解　因为

所以

3．求

分析　这是∫R（sinx）dx 型积分，可化为有理函数的积分．

解法一　令tan＝u，则sinx＝，dx＝du，于是

4．求

分析　这是∫R（sinx，cosx）dx型积分，可考虑用半角代换，但是应尽量选取简单的方法求解．

解　原式＝，下面用两种方法求积分．

方法一　因被积函数关于sinx是奇函数，所以可令cosx＝t，于是

方法二　用凑微分法，则

5．计算

6．求

分析　进行积分计算时应尽量使被积函数变得简单，易于计算，这里只要对被积函数进行分项即可．

7．求

分析　为使被积函数简单化，可直接去根号．

解　令＝u，即x＝－ln（1－u2），则

8．计算

分析　椐本题特点首先可化为两个定积分之差，然后再分别积分．

所以

9．计算

解　由奇、偶函数定积分的性质知

注　此题也可令x＝2sint，去根号后再积分．

10．

解法二　令x＝－t，则dx＝－dt，得

从而

解法三　令tan＝t，则

11．计算

解　原式＝

注　最后一个积分不能写成

12．计算

解法一　这是以x＝1为奇点的反常积分，令x＝sint，则

13．计算

分析　这是反常积分，奇点为x＝0．

解法二　因为

所以

14．求反常积分

分析　首先进行拆项，求出原函数，再运用反常积分收敛的定义可得．

15．求定积分sin（lnx）dx．

分析　采用换元积分法和分部积分法即可解．

解　令x＝et，则dx＝etdt．且当x＝1时，t＝0；x＝e时，t＝1．所以

16．求不定积分

分析　利用三角函数有关公式可简化计算．(https://www.xing528.com)

17．求定积分

解　应用奇函数的定积分性质，有

所以

18．计算定积分

分析　将被积函数进行拆项．

解　因为所以

19．计算反常积分ln（1－x）dx．

分析　需要注意x＝1是奇点，因此这是一个反常积分，可根据反常积分的定义进行计算．

20．计算不定积分

分析　先利用分部积分法，再利用换元积分法．

解　由分部积分法，得

对积分，令＝t，x2＝1－t2，则xdx＝－tdt，于是

所以

21．若f（x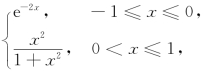）＝求f（t－1）dt．

分析　将所求积分化为在区间［－1，1］上的积分．

解　令t－1＝x，于是

注　此题也可先求出f（t－1）的表达式，再计算积分，读者不妨一试．

22．计算f（x）dx，其中f（x）满足f（x）＝f（x－π）－cosx，且f（x）＝x2，x∈［0，π）．

分析　为了计算积分，最好能求出f（x）的表达式，也可考虑由已知条件判断f（x）是否具有周期性．

解　因为

f（x）＝f（x－π）－cosx

所以

f（x＋π）＝f（x）＋cosx

于是

f（x＋2π）＝f（x＋π）－cosx＝f（x）

即f（x）以2π为周期，所以

首先

其次对I2，令x＝t＋π，得

所以

注　此题也可先求出f（x）在［π，3π］上的表达式

再计算积分．

23．设函数f（x）可导，其反函数为g（x），f（0）＝，并且f（x）与g（x）满足关系式dt，求f（1）．

解　对dt两边求导，得g［f（x）］f′（x）＝，即

所以

24．求极限

分析　这个极限是“”型未定式，可用L'Hospital法则．但对分子求导时，不能简单地用变上限定积分求导公式，因为在积分号下还含有参变量x，要先将积分号下的x 变到积分限上或积分号外，再求导．

25．设f（x）在（－1，1）内连续，在x＝0处可导，且f（0）＝0，f′（0）＝1，求极限

解　令x2－t2＝u，则tf（x2－t2）dt＝f（u）du，于是

26．求极限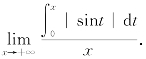

分析　此极限是型不定式，但不能用L'Hospital法则来解决．请读者考虑这是为什么．

由于

且当x→＋∞时n→∞，故由夹逼定理得

27．设f（x）＝x（x≥0），g（x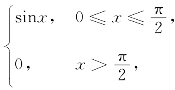）＝分别求当0≤x≤与x>时积分f（t）g（x－t）dt的表达式．

解　设u＝x－t，当0≤x≤时，有

当x＞时，有

于是