高等数学试题分析(2017)：填空题解析及计算方法

1．已知e－x是f（x）的原函数，则f（lnx）dx＝________．

解　设lnx＝t，则x＝et，于是

2．若＝arcsinx＋C，则＝_________．

解　首先利用不定积分的概念求出f（x）的表达式．

因为xf（x）＝（arcsinx）′＝从而

3．xsint2dt＝_________．

解　除了积分下限是x的函数外，被积函数也含有x，此时不能直接用变限定积分的求导公式，需设法将被积函数中的x移至积分号外或积分限上，然后再求导．即有

4．已知函数f（x）在［a，b］上连续可微，且f（a）＝f（b）＝0（x）dx＝1，则（x）dx＝_________．

解　利用分部积分法得

5．f（x）＝dt在区间________内单调增加，曲线y＝f（x）在区间_________内向下凸．

解　分别利用一阶和二阶导数研究函数的单调性和曲线的凸性．可得

当x∈时，f′（x）＞0，f（x）单调增加；

当x∈（－∞，－2）时，f″（x）＞0，曲线y＝f（x）向下凸．

6．若，则dx＝________．

解　利用分部积分法，则

7．dx＝________．

分析　可以有多种解法，这里列举两种．

注　原式≠dx，因为右边两积分都发散．

8．dx＝________．

解　由奇（偶）函数定积分的性质，得(https://www.xing528.com)

作变量代换x＝2sinθ，则

所以

9．dx＝________．

解　原式＝

所以

10．cos5xdx＝_________．

解　因为cos5x 关于点对称，所以积分xdx＝0．

11．dx＝________．

解

12．若一汽车以速度v（t）＝27－3t2（m／s）沿直线做减速运动，则从时刻t＝0到汽车停下所行驶的距离为_________m．

解　由定积分的物理意义，路程v（t）dt，其中T为汽车从时刻t＝0到停下所用的时间．令v（t）＝0，得t＝3，即T＝3，于是所求距离

13．设可导函数y＝y（x）由方程xsint2dt确定，则＝________．

解　当x＝0时，y＝0．又

将x＝0，y＝0代入，得y′（0）＝－1．

14．曲线段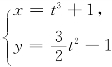（0≤t≤1）的弧长是________．

16．设f（x）＝＝________．

17．设f（t）dt＝lnx，其中f（t）为连续函数，则f（10）＝_________．

解　由题可得

令x＝3，得f（10）＝