高等数学试题分析(2017)练习题解答

1．已知函数f（x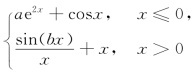）＝可导，试求常数a和b 的值．

2．设y＝arctan＋e［f（cosx）］2，其中f 可导，求

3．设y＝y（x）是由方程x2＋y2－yexy＝2所确定的隐函数，求曲线y＝y（x）在点（0，2）处的切线方程．

4．试确定常数a和b 的值，使得曲线y＝x2＋ax＋b和2y＝－1＋xy3在点（1，－1）处相切，并求切线方程．

5．设y＝y（x）是由方程x＋y＝arctan（x－y）所确定的隐函数，求导数

9．设y＝sin（f（x2）），其中函数f 具有二阶连续导数，求

10．设f（x）＝，求f（n）（x）．

11．设f（x）＝，求f（n）（x）．

12．设y＝x2e3x，求y（10）（x）．

13．设f（x）＝（x2＋x）sin2x，求f（10）（x）．

14．设函数f（x）＝且f″（0）存在，试确定常数a，b，c．

15．设函数f（x）＝

（1）求f（x）的表达式；

（2）讨论f（x）的连续性及可导性．

16．求函数y＝ln（ex）的单调区间及其图形的下凸区间．

17．求函数f（x）＝的极大值．

18．在曲线y＝e2x上求一点，使该点处的切线通过原点（0，0）．

19．计算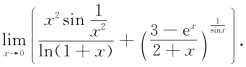

20．已知f″（0）＝2，且当x≠0时f（x）≠0，如果极限＝0，求极限

21．试确定方程ex＝ax2（a＞0）的根的个数，并指出每一根所在的范围．

22．设函数f在［0，1］上可微，对于［0，1］上的任一点x，函数f的值都在开区间（0，1）内，且f′（x）≠1，证明：在（0，1）内有且仅有一个x，使f（x）＝x．

23．设在［1，＋∞）上f″（x）≤0，且f（1）＝2，f′（1）＝－3，证明：方程f（x）＝0在（1，＋∞）内有且仅有一个实根．

24．设f 在［0，1］上连续，在（0，1）内可导，且f（1）＝0，证明：至少存在一点ξ∈（0，1），使3f（ξ）＋ξf′（ξ）＝0．

25．设函数f（x）在［0，1］上二阶可导，且f（1）＝f（0），证明：至少存在一点ξ∈（0，1），使f″（ξ）＝

26．设f（x）在［a，b］上连续，在（a，b）内二阶可导，且f（a）＝f（b）＝f（c）＝0，其中c∈（a，b）．证明：

（1）至少存在两个不同的点ξ1，ξ2 ∈（a，b），使得f′（ξi）＋f（ξi）＝0，i＝1，2；

（2）存在ξ∈（a，b），使得f″（ξ）＝f（ξ）．(www.xing528.com)

27．设函数f（x）在闭区间［a，b］上连续，在开区间（a，b）内可导，且f（a）＝b，f（b）＝a．证明：

（1）至少存在一点c∈（a，b），使得f（c）＝c；

（2）至少存在互异的两点ξ，η∈（a，b），使得f′（ξ）·f′（η）＝1．

28．已知函数f（x）在闭区间［0，3a］（a＞0）上连续，在开区间（0，3a）内可导，且f（3a）＝f（a）＜f（0）＜f（2a），试证明：至少存在一点ξ∈（0，2a），使得

f′（ξ）＝f′（ξ＋a）

29．设f（x）在闭区间［a，b］上具有一阶连续导数，在开区间（a，b）内二阶可导，且f（a）＝f（b），f′＋（a）f′－（b）＞0，试证：至少存在一点ξ∈（a，b），使得f″（ξ）＝0．

30．设f（x）在（a，b）内二阶可导，且对∀x∈（a，b），f″（x）＞0，证明：对任意的x1，x2∈（a，b），且x1≠x2及λ∈（0，1），恒有

f（λx1＋（1－λ）x2）＜λf（x1）＋（1－λ）f（x2）

31．已知函数f（x）在闭区间［0，1］上存在二阶导数，且f（1）＝0，又f（x）在处取得最小值－3，证明：存在一点ξ∈（0，1），使f″（ξ）≥24．

32．设f（x）在［a，b］上连续，在（a，b）内可导，且ab＞0，证明：∃ξ，η∈（a，b），使得f′（ξ）＝

33．求下列函数的极限：

34．证明不等式：ex≥1＋（x≥0）．

35．在曲线y＝1－x2（0＜x＜1）上求一点P（x0，y0），使过该点的切线与两坐标轴所围三角形的面积最小．

36．证明：当x≥0时，有

（1＋x）2（2ln（1＋x）－1）＋1≥4xarctanx－2ln（1＋x2）

37．设p＞1，q＞1，且＝1，证明：当x＞0时≥x．

38．设L（x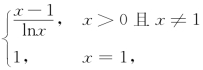）＝证明≤L（x）≤（x＞0）．

39．证明：当x>0时，x2＋1＞lnx．

40．在抛物线y＝x2上求一点P（a＞0），使弦PQ 的长度最短，并求最短长度，其中Q 是过点P 的法线与抛物线的另一个交点．

41．设有一工厂生产某种产品，除固定成本4000元外，每件产品成本为13元．根据经验，售出的产品数q与产品单价p 的关系为p＝49－0．2，问要获利最大，产品应如何定价？

42．落在平静水面上的石头会使水面产生同心圆形波纹，若最外一圈半径的增长率总是6m／s，问2s末受到扰动的水面面积的增大率为多少？

43．如果以每秒50cm3匀速给一个气球充气，假设气球内气压保持常值，且形状始终为球形，问当气球的半径为5cm 时半径增加的速率是多少？

44．（1）证明不等式

（2）设xn＝－lnn，利用单调有界原理证明数列｛xn｝收敛．

45．证明：函数f（x）＝ln（1＋x2）在（－∞，＋∞）上一致连续．