高等数学试题分析(2017)：求f在x=0处的连续性和可导性

1．设f（x）＝

（1）问a 当取何值时，f（x）在x＝0 处连续？

（2）在（1）的条件下，f（x）在x＝0处是否可导？若可导，求f′（x）．

解　（1）若要f（x）在x＝0处连续，只要

（2）当a＝－时，利用L'Hospital法则可得

当x ≠0时，由求导法则得

综上，有

2．设f（x）＝，讨论f（x）的可导性，并在可导点处求f′（x）．

解　由于

当x>0时，f′（x）＝0；当x＜0时，f′（x）＝；而当x＝0时，因为

所以f（x）在x＝0处不可导．综上所述，得f′（x）＝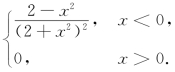

3．设y＝y（x）是由方程组所确定的函数，求

分析　本题考查参数方程求导法，其中由第二个方程确定隐函数y＝y（t）．

解　方程tey＝y两边对t求导，得ey＋tey，整理得＝由x＝t2＋2t，得＝2t＋2．所以

又＝1，于是

4．求极限

分析　这是“∞－∞”型未定式，可化为型未定式后用L'Hospital法则．

解　原式＝

5．求极限

解法一　重复用L'Hospital法则，则

解法二　利用Taylor公式，则

6．求一个二次多项式，使得当x→0 时，此多项式与函数secx 之差为x2的高阶无穷小．

解　设这个二次多项式为P（x）＝ax2＋bx＋c，由于此多项式与secx之差为无穷小量，即

由此得c＝1．又要使多项式与函数secx 之差为x2的高阶无穷小，即要使

即

由此得b＝0．因为

所以a＝．于是所求二次多项式为P（x）＝x2＋1．(www.xing528.com)

7．求函数f（x）＝ln（1＋x2）－arctan（x＜0）的极值及曲线y＝f（x）向下凸的区间．

解　先求f′（x），得f′（x）＝，令f′（x）＝0，得唯一驻点x＝－1．当x＜－1时，f′（x）＜0；当－1＜x＜0时，f′（x）＞0．所以x＝－1是f（x）的极小值点，且极小值为．又因f″（x）＝，令f″（x）＞0，得曲线的下凸区间为（－1－，0）．

8．设曲线方程为y＝xx＋，求曲线上横坐标x＝1点处的法线方程．

解　y′＝xx（1＋lnx）－，所以曲线在横坐标x＝1点处的切线斜率为，法线斜率为－2．又当x＝1时，y＝3，所以所求的法线方程为

y－3＝－2（x－1），　即　2x＋y＝5

9．设函数y＝y（x）由方程2y3－2y2＋2xy－x2＝1所确定，试求它的驻点，并判断它是否是极值点．如果是极值点，是极大值点还是极小值点？

解　方程两端对x 求导，得

6y2　y′－4yy′＋2y＋2xy′－2x＝0

即令y′＝0，得y＝x≠0，代入原方程，有2x3－x2－1＝（2x2＋x＋1）（x－1）＝0，得唯一驻点x＝1，此时

y3－y2＋y－1＝（y2＋1）（y－1）＝0

故y（1）＝1．又因为＞0，所以x＝1是唯一驻点，且是极小值点．

10．由Lagrange中值定理知ex－1＝xeθx，求

解　由条件得θ＝（x ≠0），所以

11．设函数y＝y（x）由参数方程所确定，试求

12．写出f（x）＝xlnx在x＝1处的带有Lagrange余项的三阶Taylor公式．

解　因为f（1）＝0，f′（1）＝1，f″（1）＝1，f‴（1）＝－1，f（4）（x）＝，所以

13．求极限

解　因为

利用L'Hospital法则，得

因此

14．求极限

解　利用Taylor公式，有

15．求极限

解　当x→＋∞时，→0＋，应用L'Hospital法则，则

16．求极限