高等数学试题分析(2017)-单项选择题解析

1．设f（x）＝，－∞＜x＜＋∞，则此函数是（　）

（A）有界函数　（B）奇函数　（C）偶函数　（D）周期函数

解　根据奇、偶函数及周期函数的定义及sinx 的性质立即可以否定（B），（C），（D），故选（A）．或者由｜f（x）｜＝≤1，x∈（－∞，＋∞），可知f 是（－∞，＋∞）上的有界函数．

2．极限（　）

（A）不存在　（B）等于5　（C）等于3　（D）等于0

解　利用已知极限＝1及极限的四则运算法则，有

或者利用重要极限＝e及连续函数求极限的法则可得

3．设f（x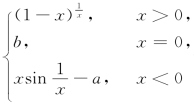）＝在x＝0处连续，则（　）

（A）a＝b＝e　（B）a＝b＝e－1

（C）a＝－b＝e－1　（D）a＝－b＝－e－1

解　本题考查连续的概念．根据题意，有

故应当选（D）．

4．设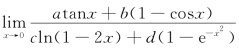＝2，其中a，b，c，d为常数，a2＋c2≠0，则必有（　）

（A）a＝－4c　（B）a＝4c　（C）b＝－4d　（D）b＝4d

解　此题是已知函数f的极限值，要确定f中所含常数的关系，利用常用的一些重要极限和极限的运算法则即可解决．因为

所以a＝－4c．

5．设函数f（x）＝（n∈N＊），则f（x）（　）

（A）不存在间断点　（B）存在间断点x＝1

（C）存在间断点x＝－1　（D）存在间断点x＝0

解　写出f（x）的表达式，即

可知x＝1是间断点．

6．设f（x），g（x）在（－∞，＋∞）内有定义，f（x）为连续函数，且f（x）≠0，g（x）有间断点，则（　）

（A）g（f（x））必有间断点　（B）［g（x）］2必有间断点

（C）f（g（x））必有间断点　（D）必有间断点

解　当f 的值域中不含g 的间断点时，g（f（x））连续，故（A）不对；当

时，［g（x）］2＝1连续，所以（B）也不对；当f 为常值函数时，f（g（x））连续，因此（C）不对；（D）是对的，可用反证法证明，留给读者．

7．设当x→x0时，α（x），β（x）都是无穷小（β（x）≠0），则当x→x0时，下列表达式中不一定为无穷小量的是（　）(www.xing528.com)

（A）　（B）α2（x）＋β2（x）sin

（C）ln（1＋α（x）·β（x））　（D）｜α（x）｜＋｜β（x）｜

解　可取α（x）＝x，β（x）＝x3，易知选（A）．

8．设f（x）＝，若f（x）在（－∞，＋∞）连续，则常数a＝（　）

（A）5　（B）4　（C）　（D）

解　先求极限得到f（x）的表达式，即

再由函数在x＝2处连续知a＝

9．极限（　）

（A）不存在但不为∞　（B）等于2

（C）等于0　（D）为∞

解　因为＝0，所以选（A）．

10．当x→0时，x－sinax 与x2ln（1－bx）是等价无穷小，则（　）

（A）a＝1，b＝－　（B）a＝1，b＝

（C）a＝1，b＝－　（D）a＝－1，b＝

解　当x→0时，因为

所以a＝1，b＝－，选（A）．

11．下列命题正确的是（　）

（A）任何两个无穷小量之比的极限必存在（极限值为有限实数或∞）

（B）若数列｛a2k－1｝和｛a2k｝都收敛，则数列｛an｝必收敛．

（C）若数列｛an｝收敛，数列｛bn｝发散，则数列｛anbn｝必发散．

（D）若数列｛an｝单调增加，数列｛bn｝单调减少，且（an－bn）＝0，则＝

解　本题考查数列（函数）极限的有关性质．（A），（B），（C）都是错的，反例如下：

（A）当x→0时，f（x）＝xsin，g（x）＝x都是无穷小量，但＝sin，当x→0时不存在极限；

（B）设an＝（－1）n，则｛an｝不收敛，但｛a2k－1｝收敛于－1，｛a2k｝收敛于1；

（C）设an＝，bn＝n，则anbn＝1，｛anbn｝收敛于1．

而选项（D），由题设知｛an－bn｝单调增加，又（an－bn）＝0，从而知an≤bn，且an≤b1，bn≥a1，因而数列｛an｝单增有上界，数列｛bn｝单减有下界，因而都收敛．再由（an－bn）＝0得知＝．故应选（D）．