格林公式及应用概述-高等数学及其应用（下）

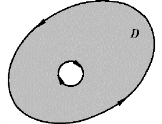
图9.47

对平面区域D 的边界曲线L,规定正向如下:当观察者沿L 的这个方向行走时,D 总在它的左边.如图9.47 所示,D 是边界曲线L 及l 围成的复连通区域,作为D 的正向边界,L 的正向是逆时针方向,而l 的方向是顺时针方向.

定理9.1　设闭区域D 由分段光滑曲线L 围成,函数P(x,y)和Q(x,y)在D 上具有一阶连续的偏导数,则

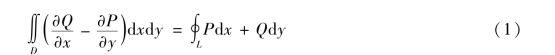
其中,L 是D 的取正方向的边界曲线.此公式称为格林公式,为方便记忆也可写为

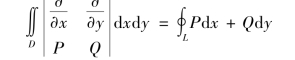
证　首先设闭域D 的边界曲线L 与任一平行于坐标轴的直线至多交予两点,如图9.48 所示.设

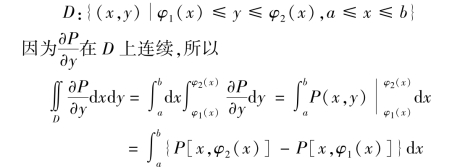
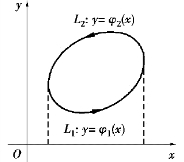
图9.48

另一方面,由对坐标曲线积分的性质及计算方法,有

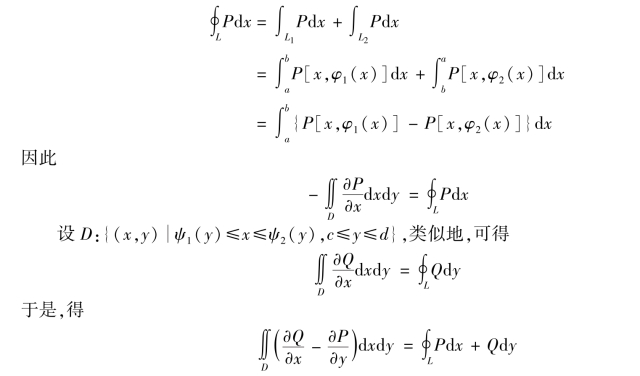
如果边界曲线L 与平行于坐标轴的直线的交点多于两个,或者是复连通区域,则可把D分成若干部分,使每部分是单连通区域,并且每部分的边界曲线与平行于坐标轴的直线的至多交于两点.同样,可证明格林公式成立.

在式(1)中,取P= -y,Q=x,得

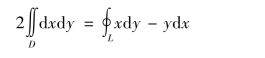
所以区域D 的面积

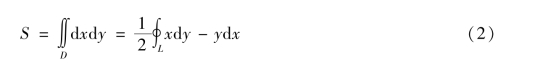(www.xing528.com)

其中,L 是D 的边界曲线,且取正方向.

例1　利用曲线积分计算椭圆x=a cos t,y=b sin t 所围成图形的面积.

解　由式(2)得

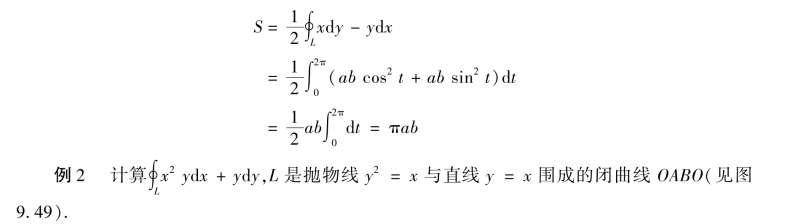
解　本题可用上节方法计算,也可利用格林公式计算.

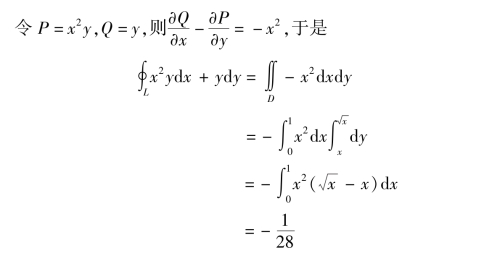
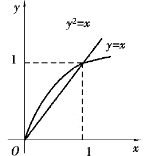
图9.49

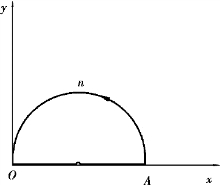
图9.50

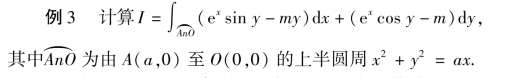
解　补充O 到A 的直线段,则AnOA 成为闭曲线L,且L的方向为区域D 的正方向(见图9.50).由格林公式,取

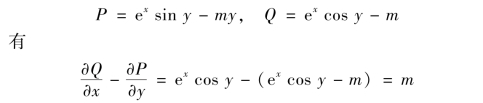
于是

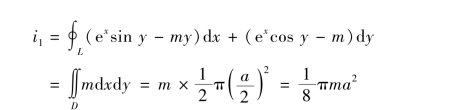
又因为在直线OA 上,y=0,dy=0,x 由0 变到a,故

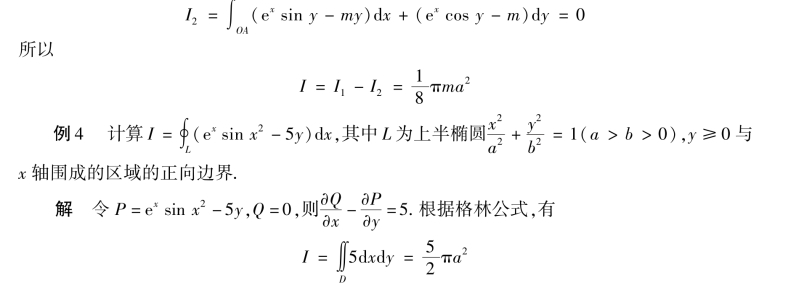
由例3 和例4 可知,在对坐标的曲线积分中,应用格林公式可化难为易,大大地减少计算量.