高等数学及应用第二类曲面积分

通常遇到的一般曲面都是双面的.例如,由方程z =z(x,y)所确定的曲面就有上侧与下侧之分,而方程x=y2 +z2 确定的平面有前侧和后侧之分,球面x2 +y2 +z2 =R2,有内侧与外侧之分.

在讨论对坐标的曲面积分时,需要指定曲面的侧.例如,对于曲面z =z(x,y),如果取它的法向量n 的指向朝上,就认为取定曲面的上侧,另一面则为下侧;又如,对球面,如果取它的法向量n 的指向朝外,就认为取定曲面的外侧,另一面则为内侧.

引例5　求流向曲面指定侧的流量

不可压缩的液体在单位时间内,流向曲面z 指定侧的体积称体积流量,简称流量.

设流速

将曲面z 任意分成n 个子域ΔSi(i =1,2,…,n),简记ΔS,也表示子域的面积.在每个子域上任取(x,y,z)(见图9.44),用该点处的流速代替子域上的流速,其上指定侧的法向量为n =cos αi +cos βj +cos γk,则在ΔS 上的流量ΔW 近似值为

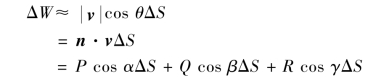
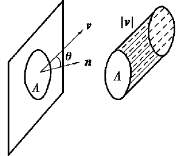
图9.44

其中,θ 是n 与v 的夹角,得

这样的和式的极限还会在其他问题中遇到,由此引入第二类曲面积分的概念.

1.第二类曲面积分的概念与性质

定义9.6　设函数P=P(x,y,z)在有向曲面z 上有定义,其法向量

2.第二类曲面积分的计算

设有向曲面Σ 在xOy 坐标面上的投影为D,Σ 的方程z=z(x,y),则

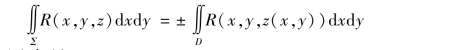
其中,上侧取正好,下侧取负号.

类似地,有下列两个公式:

当有向曲面Σ 的方程为y=y(x,z)时,则

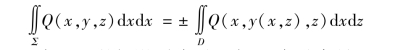
其中,D 为曲面Σ 在xOy 坐标面上的投影,右侧取正好,左侧取负号.

当有向曲面Σ 的方程为x=x(y,z)时,则

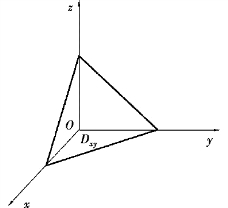
图9.45(www.xing528.com)

解　把有向曲面分成6 部分:

Σ1∶z=a(0≤x≤a,0≤y≤a)的上侧;

Σ2∶z=0(0≤x≤a,0≤y≤a)的下侧;

Σ3∶x=a(0≤y≤a,0≤z≤a)的前侧;

Σ4∶x=0(0≤y≤a,0≤z≤a)的后侧;

Σ5∶y=a(0≤x≤a,0≤z≤a)的右侧;

Σ6∶y=0(0≤x≤a,0≤z≤a)的左侧.

除Σ3,Σ4 外,其余4 部分曲面在yOz 平面上的投影为零(见图9.46),因此

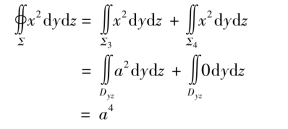
图9.46

类似地,可得

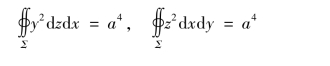
所以

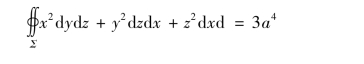
习题9.6

1.计算I =∫L(x + y)dx,其中L 为:

(1) 沿y = 2x 由点O(0,0) 到A(1,2) 的直线段;

(2) 由O(0,0) 经x 轴到B(1,0),再经直线x = 1 到A(1,2);

(3) 由B(- R,0) 经半径为R 的上半圆周x2 + y2 = R2 到A(R,0).2.计算I =∫Lxdy - ydx,其中L 为:

(1) 沿y = x 由点O(0,0) 到点B(1,1) 的弧段;

(2) 沿y = x2 由点O(0,0) 到点B(1,1) 的弧段;

(3) 沿y = x3 由点O(0,0) 到点B(1,1) 的弧段.