【摘要】:(1)如果曲线L 的方程以y=y(x)给出,设P(x,y),y′(x)均连续,曲线L 的起点的横坐标为a,终点的横坐标为b(b 不一定大于a).因为被积函数P(x,y)中的(x,y)是在曲线L 上变化,所以它们有关系y=y(x).由定义可得同理,曲线L 的方程以x=x(y)给出,得其中,c 为曲线L 起点的纵坐标,d 是其终点的纵坐标(d 不一定大于c).其中,曲线L 的起点和终点所对应的参数值分
(1)如果曲线L 的方程以y=y(x)给出,设P(x,y),y′(x)均连续,曲线L 的起点的横坐标为a,终点的横坐标为b(b 不一定大于a).因为被积函数P(x,y)中的(x,y)是在曲线L 上变化,所以它们有关系y=y(x).由定义可得
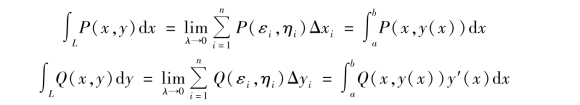
同理,曲线L 的方程以x=x(y)给出,得
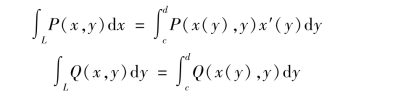
其中,c 为曲线L 起点的纵坐标,d 是其终点的纵坐标(d 不一定大于c).

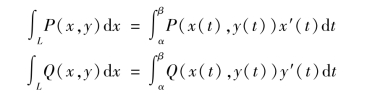
其中,曲线L 的起点和终点所对应的参数值分别为α 和β.
例1 计算∫Ly2dx,其中L 为:
(1)半径为a,圆心为原点,按逆时针方向绕行的上半圆周;
(2)从点A(a,0)沿x 轴到点B(-a,0)的直线段(见图9.42).
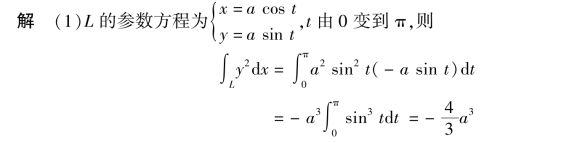
(2)L 的方程为y=0,x 由a 变到-a,则(https://www.xing528.com)
![]()
从此例可知,被积函数相同,起点和终点也相同,但沿不同的路径得出的积分值并不相等,即此积分与积分路径有关.
例2 计算I =∫L2xydx + x2dy,其中L 为:
(1) 抛物线y=x2 上从(0,0)到(1,1);
(2)有向折线从(0,0)到(1,0)再到(1,1)(见图9.43).
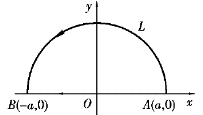
图9.42
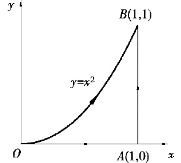
图9.43

解 将L 表示为参数方程x=R cos θ,y=R sin θ.由A 以逆时针方向再回到A,起点A 对应t=0,再回到A(终点)对应t=2π.当t 由0 变到2π 时,对应的点恰好由点A 沿逆时针转一圈回到A,所以
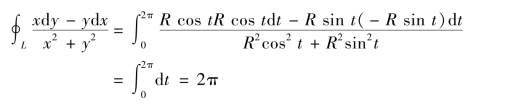
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




