1.质心

参照质点系的质心,应用元素法求平面板的质心.
设平面板在xOy 平面上占有界闭区域为D,平面板的密度函数ρ(x,y)≥0 是连续的.D 上任取一小闭区域dσ,小闭区域上的任一点(x,y),小闭区域的质量可近似看成集中在点(x,y)上,可求得静力矩元素dMx =yρ(x,y)dσ,dMy =xρ(x,y)dσ.
求和得平面板对x 轴和y 轴的静力矩分别为
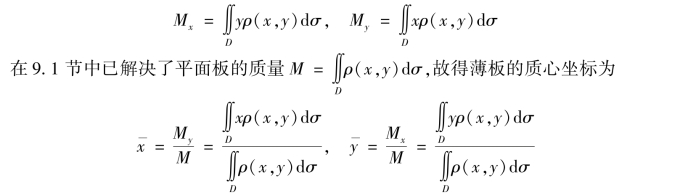
特别地,如果薄板是均匀的(面密度是常数),则均匀薄板的质心的坐标为

其中,M=ρV 是Ω 的质量.
例4 求位于两圆ρ=2 sin φ 和ρ=4 sin φ 之间的均匀薄板的形心.
解 如图9.33 所示,因图形关于y 轴对称,故形心的x 坐标为零.其形心的y 坐标为

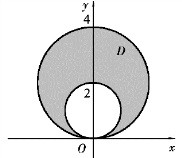
图9.33
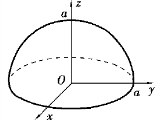
图9.34
由公式得
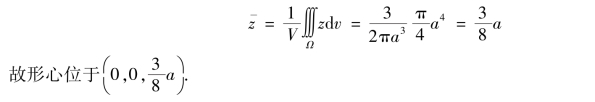
2.转动惯量
设xOy 平面上由n 个质点M1(x1,y1),M2(x2,y2),…,Mn(xn,yn)构成一个质点系,它们的质量为m1,m2,…,mn.由力学可知,该质点系对x 轴以及对y 轴的转动惯量分别为
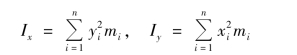
参照质点系的转动惯量,应用元素法求质量呈连续分布的薄板的转动惯量.
设一薄板在xOy 平面上占有界闭区域为D,面密度为ρ(x,y)≥0,且在D 上是连续的,求薄板对x 轴的转动惯量Ix 以及对y 轴的转动惯量Iy.(https://www.xing528.com)
由元素法,在D 上任取一小闭区域dσ(也是小闭区域的面积),小闭区域上的任一点(x,y).ρ(x,y)在D 上连续,所以dσ 的质量近似等于ρ(x,y)dσ,且质量可近似看成集中在点(x,y)处.于是,可得对x 轴的转动惯量Ix 和对y 轴的转动惯量Iy 元素
![]()
求和可得薄板分别对x 轴,y 轴的转动惯量,则
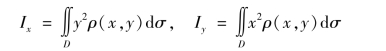
同理,根据转动惯量的物理意义和类似的推导,可得空间物体Ω 分别对x 轴、y 轴、z 轴的转动惯量.设Ω 上的密度函数为ρ(x,y,z)≥0 且连续,则
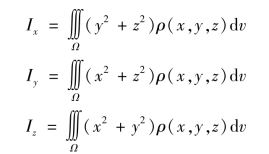
例6 求半径为a 的均匀半圆薄板对其直径边的转动惯量.
解 其质量是分布均匀的,设面密度为常数k.建立直角坐标系,则薄板占的区域如图9.35 所示.
D:x2 +y2≤a2,y≥0,根据公式对x 轴的转动惯量
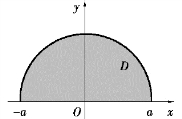
图9.35

习题9.4
1.设平面薄片所占的闭区域D 由直线x +y =2,y =x 和x 轴所围成,它的面密度ρ(x,y) =x2 +y2,求该薄片的质量.
2.计算下列立体体积:
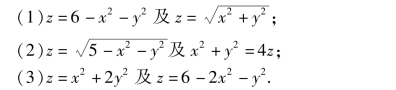
3.求曲面z=x2 +y2 在圆柱面x2 +y2 =4 内的曲面面积.
4.求球面x2 +y2 +z2 =a2 含圆柱面x2 +y2 =ax 内部的那部分面积.
5.设薄片所占的闭区域D 如下,求均匀薄片的形心:
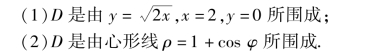
6.设薄片所占的闭区域D 如下,求指定的转动惯量:
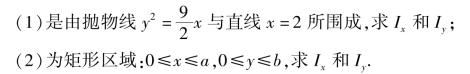
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




