计算直交圆柱体体积-V1

1.立体的体积

根据二重积分的几何意义及立体体积的可加性,应用二重积分可计算一些立体体积.

例1　求两个底圆半径都等于R 的直交圆柱面所围成的立体的体积.

图9.31

解　积分区域Ω 如图9.31 所示.设两个圆柱面的方程分别为

利用立体关于坐标面的对称性,只要算出它在第一卦限部分的体积V1,然后再乘以即可. 所求立体在第一卦限部分可看成曲顶柱体,它的底为

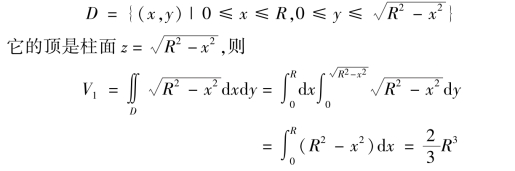
于是,所求立体体积为

解　积分区域Ω 如图9.32 所示.在球面坐标下

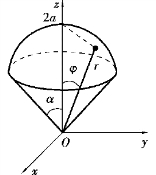
图9.32(www.xing528.com)

2.曲面的面积

设曲面Σ 由方程z=f(x,y)给出,D 为曲面Σ 在Oxy 平面上的投影区域,函数z=f(x,y)在D 上有连续的偏导数fx(x,y)和fy(x,y).求曲面Σ 的面积A.

将D 任意分成n 个小区域Δσ1,Δσ2,…,Δσn(也表示小区域的面积),在第i 个小区域Δσi 中任取一点Mi,过点Mi 作曲面Σ 的切平面Ti,以Δσi 的边界为准线,母线平行于z 轴的柱面割出曲面Σ 上的一小块曲面ΔAi(也表示相应的面积),同时这个柱面还割出切平面Ti 上的一块平面ΔTi.当Δσi 很小时,用ΔTi 近似代替ΔAi,可证曲面Σ 的面积微元,则

得曲面面积的计算公式为

同理,如果曲面Σ 由方程y=f(x,z),(x,z)∈Dzx,则曲面面积公式为

如果曲面Σ 由方程x=f(y,z),(y,z)∈Dyz,则曲面面积公式为

例3　求以R 为半径的球体表面积A.

解　将球心放在原点,建立球面方程