直角坐标系中计算二重积分

由定义可知,如果f(x,y)在D 上可积,则和式的极限存在,且与D 的分法无关.因此,在直角坐标系中,可用平行于坐标轴的直线网来分割D,除了边界处的小区域外,其余小区域都是小矩形,设其边长为Δxi,Δyi.此时,小区域的面积为

从而面积元素为dσ=dxdy,故在直角坐标系中有

由4.5 可知,基本的平面区域分为X 型区域和Y 型区域.

X 型区域D 在x 轴上的投影区间为[a,b],D 有上下两条边界曲线,下边界曲线为y =φ1(x),上边界曲线为y=φ2(x),即

其中,φ1(x),φ2(x)在区间[a,b]上连续.

X 型区域的特点是:过区间(a,b)中的点作垂直于x 轴的直线X=x,它与D 的边界至多有两个交点(见图9.4).

图9.4

Y 型区域D 在y 轴上的投影区间为[c,d],D 有左右两条边界曲线,左边界曲线x =ψ1(y),右边界曲线x=ψ2(y),即

其中,ψ1(y),ψ2(y)在区间[c,d]上连续.

Y 型区域的特点是:过区间(c,d)中点作垂直于y 轴的直线Y=y,它与D 的边界至多有两个交点(见图9.5).

设f(x,y)≥0,积分区域D 是X 型区域,即

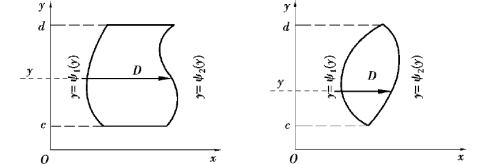
图9.5

由二重积分的几何意义:以D 为底,以曲面z =f(x,y)为顶的曲顶柱体(见图9.6)的体积V,有

再利用“平行截面面积为已知的立体的体积”的计算方法来求这个曲顶柱体的体积.

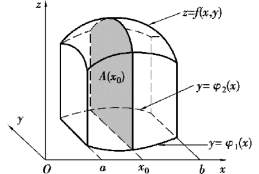
图9.6

在区间[a,b]上任意取定一点x0,作平行于yOz 面的平面x=x0.

平面x=x0 截曲顶柱体得截面为:以区间[φ1(x0),φ2(x0)]为底,曲线z=f(x0,y)为曲边的曲边梯形(见图9.6的阴影部分),其面积为

即过区间[a,b]上任一点x,且平行于yOz 面的平面截曲顶柱体所得截面的面积为

由计算平行截面面积为已知的立体体积的方法,得曲顶柱体体积为

所以

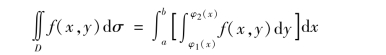
上式右端的积分称为先对y,后对x 的二次积分.就是说,首先把x 看成常数,f(x,y)为y的函数,并从φ1(x)到φ2(x)对y 计算定积分,然后把算得的结果(是关于x 的函数),在区间[a,b]上再对x 计算定积分.这个先对y 后对x 的二次积分也常记作

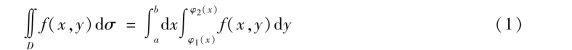
如果去掉上面讨论中的f(x,y)≥0 的限制,上式仍然成立.

类似地,如果积分区域D 是Y 型区域,即

用平行于xOz 面的平面去截曲顶柱体,则可得到

或

这是二重积分化为先对x 后对y 的二次积分.

特别地,若区域D 是一矩形,即

则

图9.7

以上的积分区域分别为X 型和Y 型的情况,其区域的边界与平行于坐标轴的直线至多有两交点,如果平行于坐标轴的直线与积分区域D 的交点超过两点(见图9.7),则需要将D 分成若干个小区域,使每个小区域的边界线与平行于坐标轴的直线的交点至多有两个.然后再应用积分对区域的可加性计算积分.

根据上述讨论,计算二重积分可归结为计算二次定积分,关键是如何根据积分区域选择适当的积分次序和确定积分的上下限.一般应先画出积分区域的草图,求边界曲线交点,或写出区域D 内的点所满足的不等式,即找出x,y 在区域D 上的变化范围,从小到大,从边界到边界,确定积分的上下限.

解　画出积分区域D 的草图,交点为(1,1),(2,2),(2,1).

方法1:D 视为是X 型区域(见图9.8(a)).D 在x 轴上的投影区间为[1,2],下边界线y=1,上边界线y=x,则

方法2:D 视为是Y 型区域(见图9.8(b)).D 在y 轴上的投影区间为[1,2],左边界线x=y,右边界线x=2,则

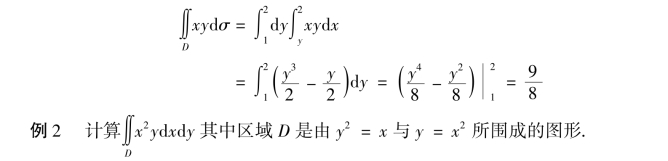
解　画出积分区域D(见图9.9).

图9.8(www.xing528.com)

图9.9

y2 =x 与y=x2 的交点是(0,0)与(1,1).

方法1:D 视为看成X 型区域

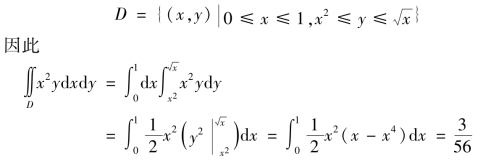
方法2:D 视为Y 型区域

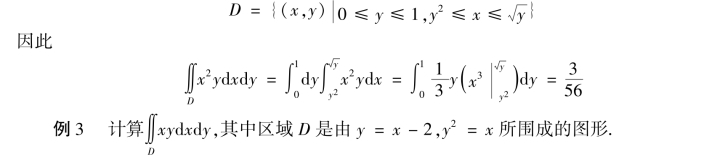
解　画出积分区域D.

求y=x-4 与y2 =2x 的交点为(4,2),(1,-1).

方法1:D 视为Y 型区域(见图9.10(a)),即

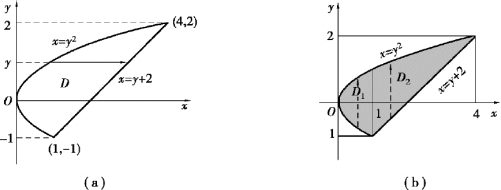
图9.10

分别在这两个区域上计算二次积分,则

这个例题说明,选择适当的二次积分次序可使二重积分的计算变得简单. 对某些二重积分,如果选择积分次序不当,会导致无法计算出来.解　画出积分区域D(见图9.12),求得交点为(0,0),(0,2),(2,2).

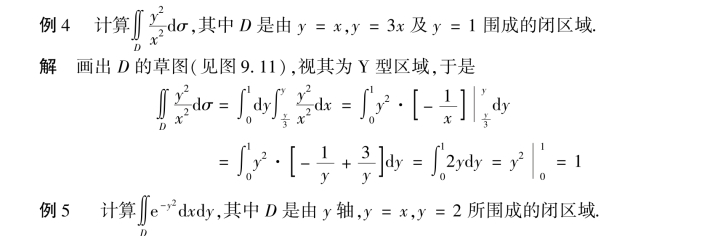
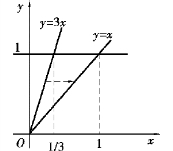
图9.11

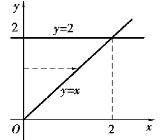
图9.12

方法1:若把D 看成X 型区域

因为

又因第一次积分中e -y2的无法计算(原函数不是初等函数),故二重积分无法计算.

方法2:把D 看成Y 型区域,有

图9.13

解　首先画出积分区域D(见图9. 13),求出交点(0,0),(1,1),(2,0).

把D 看成Y 型区域,则

所以

把D 看成X 型区域,需要作出辅助线x=1,将D 分为两个区域D1 和D2,则

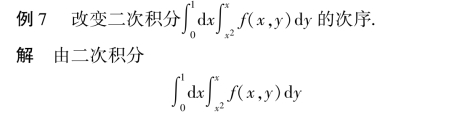
可知,x 的由0 到1,y 由y=x2 到y=x,视积分区域为X 型

画出积分区域(见图9.14).若将积分区域看成Y 型

所以

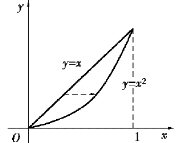
图9.14

*与定积分的对称性相仿,若积分区域关于坐标轴对称,利用被积函数的奇偶性可简化二重积分的计算.

设积分区域D 关于y 轴(x 轴)对称,即D 被y 轴(x 轴)分为左右(上下)对称的两部分D1和D2.

(1)若函数f(x,y)关于x 是奇函数,即对任何的y,都有f(-x,y) = -f(x,y),则

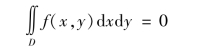
(2)若函数f(x,y)关于x 是偶函数,即对任何的y,都有f(-x,y) =f(x,y),则

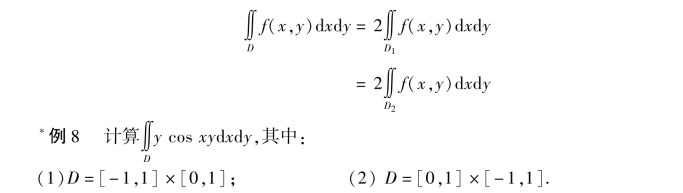
解　画出积分区域D

(1)积分区域D(见图9.15(a))关于y 轴对称,被积函数y cos xy 关于x 是偶函数,所以

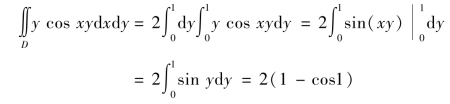
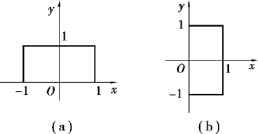
图9.15

(2) 积分区域D(见图9.15(b))关于x 轴对称,被积函数y cos xy 关于y 是奇函数,所以