在一元函数微分学中,非常重要的内容之一是复合函数的导数.设y =f(u),u =φ(x),如果u=φ(x)在点x 处可导,y=f(u)在对应的点u 处可导,则复合函数y=f[φ(x)]在点x 处可导,并且
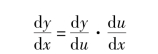
将一元复合函数的求导法则推广而得到的多元复合函数求导法则,称为链式法则.链式法则的实质仍然是函数对自变量的导数等于函数对中间变量的导数乘以中间变量对自变量的导数.
下面给出几种常见情形的复合函数的求导法则.
1.复合函数的中间变量均为一元函数的情形
定理8.4 如果函数u=φ(t)及v=ψ(t)都在点t 可导,函数z=f(u,v)在对应点(u,v)具有连续偏导数,则复合函数z=f[φ(t),ψ(t)]在点t 可导,且有
![]()
证 设t 获得增量Δt,则u=φ(t)和v=ψ(t)获得对应的增量Δu,Δv,由此函数z=f(u,v)相应地获得增量Δz.因为z=f(u,v)具有连续的偏导数,所以它在点(u,v)处可微,于是

推广 设z=f(u,v,w),u =φ(t),v =ψ(t),w =ω(t),则z =f[φ(t),ψ(t),ω(t)]对的导数为
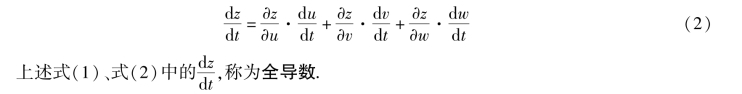
在此情形的链式公式(1)、式(2)中,函数、中间变量和自变量的关系如图8.3 所示.

图8.3
2.复合函数的中间变量均为多元函数的情形
如果函数u=φ(x,y),v=ψ(x,y)在点(x,y)处偏导数存在,函数z =f(u,v)在对应点(u,v)处也可微(具有连续偏导数),则复合函数z =f[φ(x,y),ψ(x,y)]在点(x,y)的偏导数存在,且有

推广 (1)设z=f(u)而u=φ(x,y),则z=f[φ(x,y)],有
![]()
(2)设z=f(u,v,w),而u=φ(x,y),v=ψ(x,y),w=ω(x,y),则
![]()
有
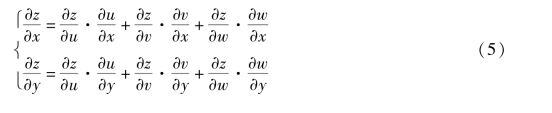
在此情形的链式式(3)、式(4)、式(5)中,复合函数、中间变量和自变量的关系如图8.4所示.

图8.4
从以上两种情形可归纳出多元复合函数链式法则求偏导数的3 个特点:
(1)所求的偏导数的个数是复合函数自变量的个数.
(2)每个偏导数均为若干个项的和,项的个数是中间变量的个数.
(3)每一项都是函数对中间变量的偏导数乘以此中间变量对自变量的偏导数.
![]()
解 画出链式图如图8.5 所示.由复合函数的微分法则,得
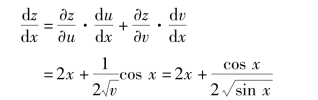
![]()
图8.5
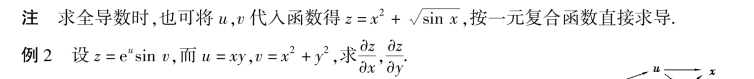
解 画出链式图如图8.6 所示.由复合函数的微分法则,得
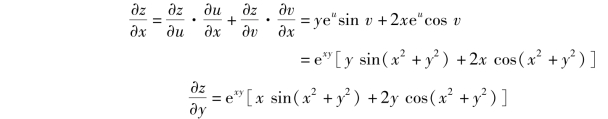
![]()
图8.6
注意 由于函数中变量的对称性,因此,上式可直接得到.
![]()
解 由复合函数的微分法则,得
 (https://www.xing528.com)
(https://www.xing528.com)
证 画出链式图如图8.7 所示.设u=x2 +y2,z=φ(u),则
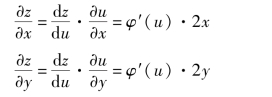
![]()
图8.7
代入左边

得证.
例5 求z=f(xy,x+y)的偏导数,其中f 具有连续偏导数.
解 画出链式图如图8.8 所示.设u=xy,v=x+y,由复合函数的微分法则,得
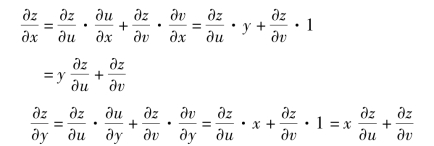
![]()
图8.8
例6 求z=f(x+y,x-y,xy)的偏导数,其中f 具有一阶连续偏导数.
解 画出链式图如图8.9 所示.设u=x+y,v=x-y,w=xy.由复合函数的微分法则,得
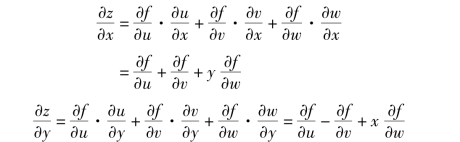
![]()
图8.9
3.复合函数的中间变量既有一元函数,又有多元函数的情形
设u=φ(x,y),v=ψ(y)在点y 可导,z=f(u,v)在对应点(u,v)可微,则复合函数z=f[φ(x,y),ψ(y)]在点(x,y)的偏导数存在,且有
![]()
4.复合函数的中间变量本身又是自变量的情形
作为情形3 的特例z=f[φ(x,y),y],u=φ(x,y),而v=y 既是中间变量又是自变量,则函数的偏导数仍然可用上式求得.
设z=f(x,y,w)u=x,v=yw=μ(x,y)时的情形(两个中间变量本身又是自变量).
如果函数w=μ(x,y)在点(x,y)偏导数存在,z=f(x,y,w)在对应点可微,则复合函数z =f[x,y,μ(x,y)]在点(x,y,w)处的偏导数存在,且有


解 设u=x,v=xy,则
![]()
理解链式法则,掌握链式公式特点,就能写出其他情形多元复合函数的偏导数公式.这里不一一列出.
对抽象函数的情形,为了书写方便,可用记号f′1,f′2 表示函数分别对第一、第二个中间变量的偏导数;类似地,引入f″11,f″12,…表示函数分别对第一个中间变量的二阶偏导数、对第一和第二个中间变量的二阶混合偏导数,其他记号以此类推.

解 令u=x+y,v=xy,利用链式法则有
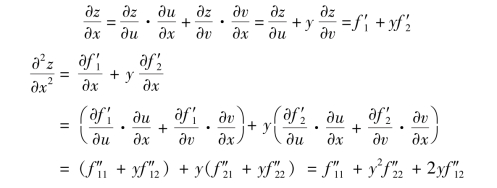
注 一般这里约定f″12 =f″21.
![]()
*5.全微分形式不变性
设z=f(u,v)具有连续偏导数,则全微分
![]()
如果z=f(u,v)具有连续偏导数,而u=φ(x,y),v=ψ(x,y)也具有连续偏导数,则
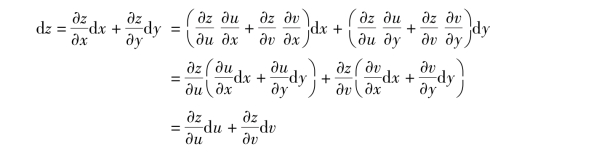
由此可知,无论z 是自变量u,v 的函数或中间变量u,v 的函数,它的全微分形式是一样的.这个性质称为全微分形式不变性.
例10 设z=eusin v,u=xy,v=x+y,利用全微分形式不变性求全微分.
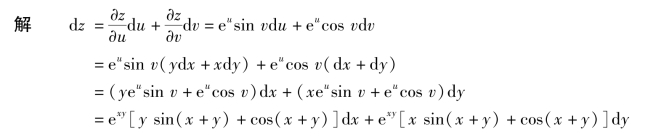
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




