在研究一元函数的变化率时,引入了导数的概念.对多元函数,同样也需要研究它的变化率问题.由于多元函数的自变量不止一个,因变量与自变量的关系比较复杂,因此,研究多元函数时,可将多元函数中的某一个自变量的取值变化,而其他变量的取值保持不变,函数关于这个变化着的自变量的变化率,就是该多元函数对这个自变量的偏导数. 如对二元函数z =f(x,y),若只有自变量x 变化,而自变量y 固定,这时它就是x 的一元函数,该函数对x 的导数,就称为二元函数z=f(x,y)对x 的偏导数.下面以二元函数为例给出偏导数定义.
1.偏导数的定义
类似一元函数微分学中因变量增量的定义,称Δxz=f(x+Δx,y) -f(x,y)为函数对x 的偏增量;Δyz=f(x,y+Δy) -f(x,y)为函数对y 的偏增量.
定义8.4 设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义,如果极限
存在,则称此极限为函数z=f(x,y)在点(x0,y0)处对x 的偏导数,记作
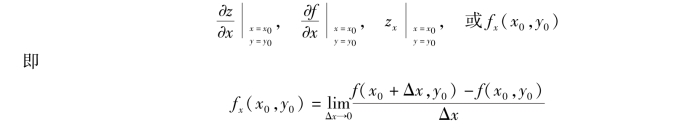
类似地,函数z=f(x,y)在点(x0,y0)处对y 的偏导数定义为
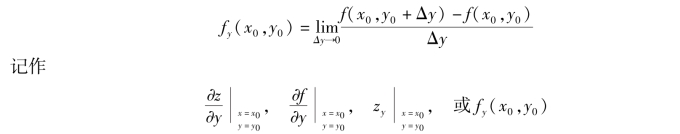
如果函数z=f(x,y)在区域D 内每一点(x,y)处对x 的偏导数都存在,那么这个偏导数就是x,y 的函数,称为函数z=f(x,y)对自变量x 的偏导函数,记作
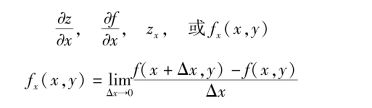
类似地,可定义函数z=f(x,y)对自变量y 的偏导函数,记作
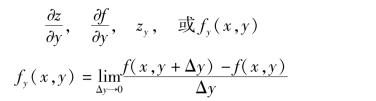
2.偏导数的几何意义
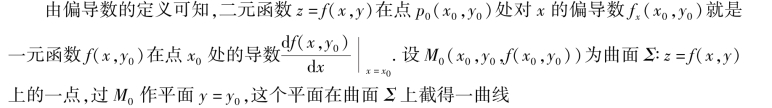(www.xing528.com)
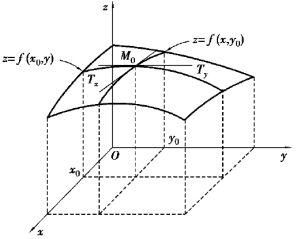
图8.2
3.偏导数的求法
偏导数的概念还可推广到二元以上的函数.例如,三元函数u=f(x,y,z)在点(x,y,z)处对x 的偏导数定义为
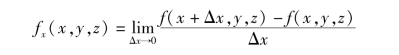
其中,(x,y,z)是函数u =f(x,y,z)的定义域的内点. 它们的求法仍旧是一元函数的微分法问题.
例1 求z=x2 +y2 -xy 在点(1,3)处的偏导数.
解 先求偏导函数
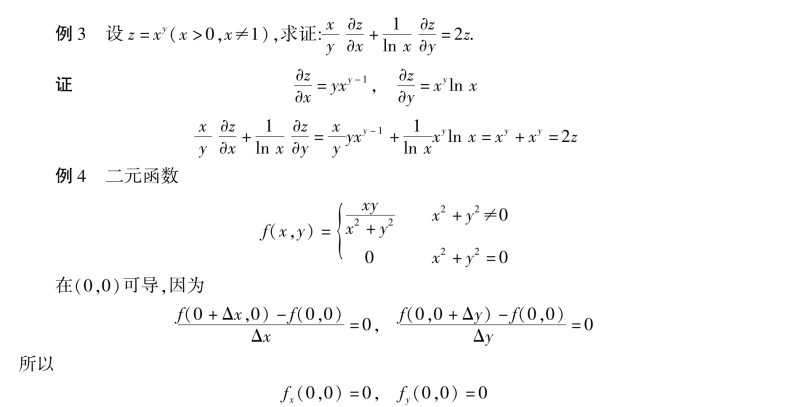
但函数f(x,y)在点(0,0)并不连续.
由例4 可知,对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
