高等数学及其应用（下）-实验二次曲面绘制

实验目的

(1)理解空间解析几何中的常用的曲面.

(2)掌握用MATLAB 绘制的空间的曲面.

实验要求

熟悉MATLAB 中图形命令mesh,meshc,meshz 等.

实验内容

1.绘制z=(1 +x+y)2 的图形.

2.画旋转抛物面z=x2 +y2.

5.分别用指令mesh,meshc,meshz 画出函数

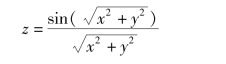
在-8≤x,y≤8 上的图形.

6.绘制函数z=3 -x2 -y2,-1≤x,y≤1 的网格图和表面图.

7.画函数x2 +y2 +z2 =1 与x2 +y2 +z2 =4.

8.画函数x2 +y2 =1 所形成的柱面与旋转曲面.

实验过程

1. ＞＞x= -4:4

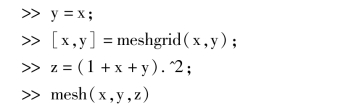
运行结果:空间曲面如图7.44 所示.

2. ＞＞x= -3:3

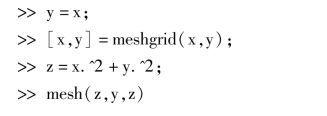
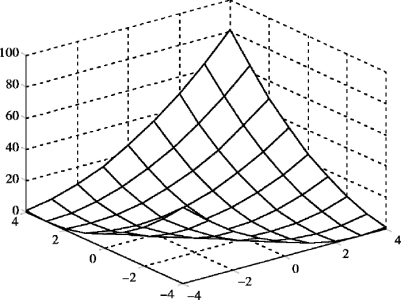
图7.44

运行结果:旋转抛物面如图7.45 所示.

3. ＞＞x=0.2:0.01:0.5

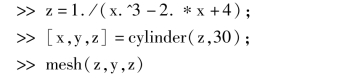
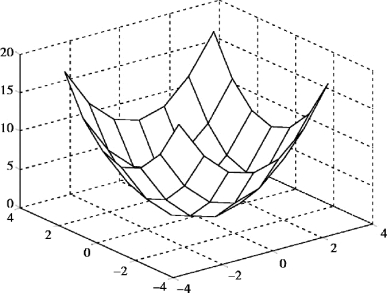
图7.45

运行结果:旋转柱面如图7.46 所示.

4. ＞＞[x,y] =meshgrid( -3:0.3:3,-3:0.3:3)

运行结果:空间图形如图7.47 所示.

(https://www.xing528.com)

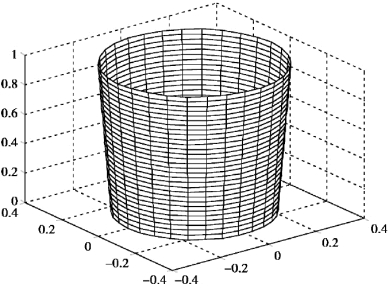
图7.46

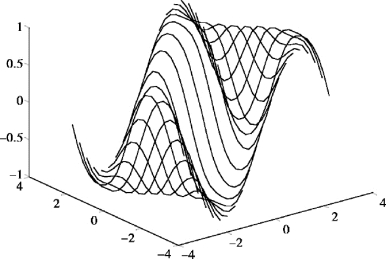
图7.47

运行结果:马鞍面图形如图7.48 所示.

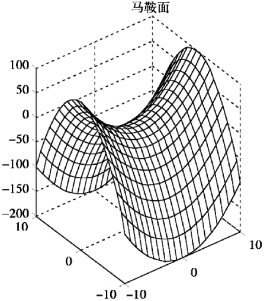
图7.48

5. ＞＞t= -8:0.3:8

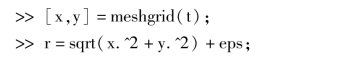
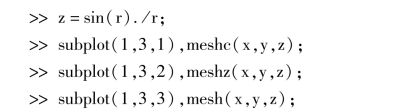
运行结果:空间图形如图7.49 所示.

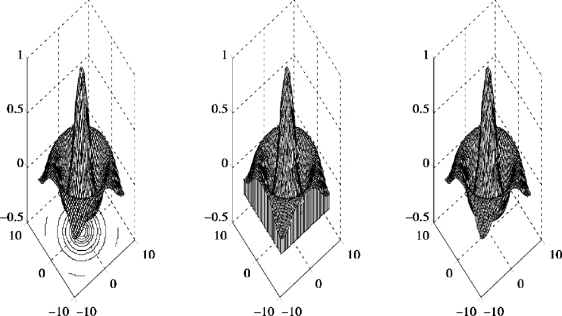
图7.49

6. ＞＞t= -1:0.1:1

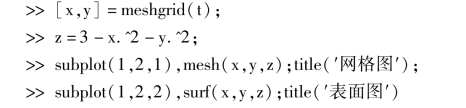
运行结果:网格图和表面图如图7.50 所示.

图7.50

7. ＞＞v=[ -2,2,-2,2,-2,2]

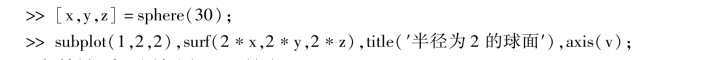
运行结果:球面图如图7.51 所示.

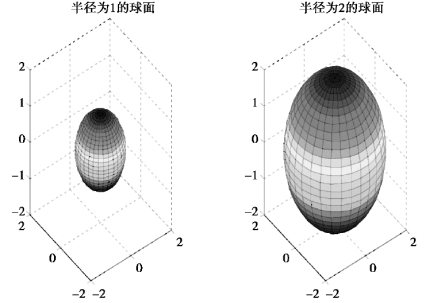
图7.51

8. ＞＞r= -1:0.1:1

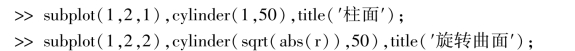
运行结果:柱面如图7.52 所示,旋转柱面如图7.53 所示.

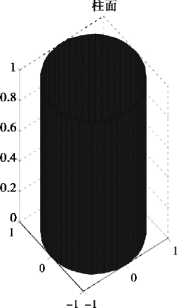
图7.52

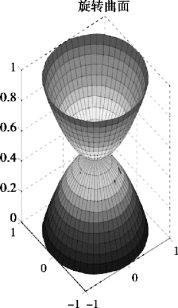
图7.53