高等数学下-常见二次曲面

由三元二次方程所表示的曲面,称为二次曲面.如前面讲过的球面、圆柱面、圆锥面及抛物柱面等都是二次曲面.相应地,三元一次方程表示的平面,称为一次曲面.在平面解析几何中,描绘曲线图形通常采用描点法.而在空间中,为描绘F(x,y,z) =0 所表示的曲面,通常采用一系列平行于坐标面的平面去截曲线,得到一系列截痕曲线,通过这些曲线的形状来确定曲面的形状.这种研究曲面的方法称为截痕法.下面利用截痕法来画出几种常用二次曲面.

1.椭球面

方程

表示的曲面(a ＞0,b ＞0,c ＞0),称为椭球面(见图7.31).

由方程(5)可知

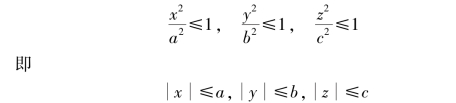
这说明椭球面(5)完全包含在一个以原点O 为中心的长方体内.a,b,c 称为椭球面的半轴.

椭球面与3 个坐标面的交线分别为

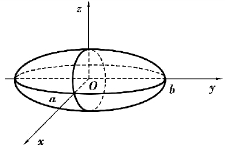
图7.31

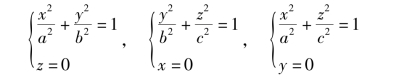
这些交线都是椭圆.

特别地,若a=b,方程(5)变为

如果a=b=c,那么方程(5)变为

它表示球心在坐标原点O、半径为a 的球面.

2.抛物面

1)椭圆抛物面

由方程

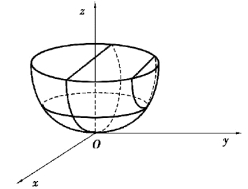
图7.32

所表示的曲面,称为椭圆抛物面(见图7.32).椭圆抛物面与xOz 坐标面和yOz 坐标面的交线分别为两条抛物线(https://www.xing528.com)

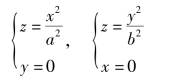
用xOy 坐标面去截椭圆抛物面所得图形是坐标原点,用z =k,(k ＞0)去截椭圆抛物面所得图形是椭圆

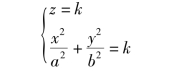
并且当k 越大,椭圆的长短轴也越长;k ＜0 时,没有图形.

如果a=b,那么方程(6)变为

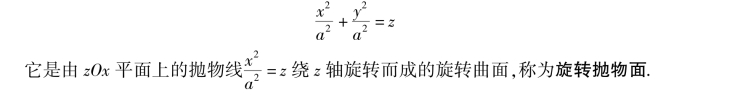
2)双曲抛物面

由方程

所表示的曲面,称为双曲抛物面或鞍形曲面.采用截痕法分析可得,它的形状如图7.33 所示.

3.双曲面

1)单叶双曲面

由方程

所表示的曲面,称为单叶双曲面.它的形状如图7.34 所示.

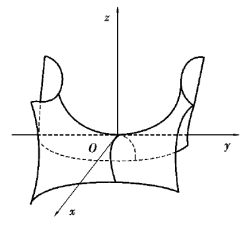
图7.33

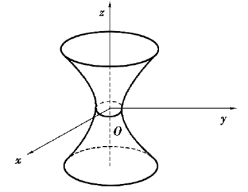
图7.34

如果a=b,那么方程(8)变为

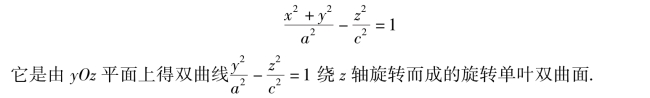
2)双叶双曲面

由方程

表示的曲面,称为双叶双曲面.它的形状如图7.35 所示.