高等数学及其应用（下）：平面的一般方程

由上述讨论可知,过点M0(x0,y0,z0)且以n=(A,B,C)为法向量的平面点法式方程为

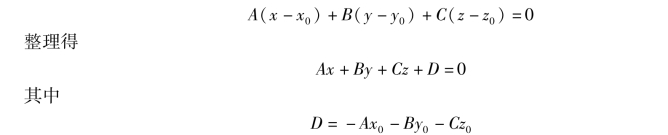
因此,任一平面都可用三元一次方程来表示.

反过来,设有三元一次方程

任取满足该方程的一组数x0,y0,z0,即

把上述两等式相减,可得与方程(2)同解的方程为

把它和平面的点法式方程(1)作比较,可知它是通过点M0(x0,y0,z0)且以n =(A,B,C)为法向量的平面方程.由此可知,任一三元一次方程(2)的图形总是一个平面.方程(2)称为平面的一般方程.其中,x,y,z 系数就是该平面的一个法向量n 的坐标,即n=(A,B,C).

例如,方程

表示一个平面,n=(3,-4,1)是这平面的一个法向量.

对一些特殊的三元一次方程,应熟悉它们的图形的特点.

(1)当D=0 时,方程(2)成为Ax+By+Cz=0,它表示一个通过原点的平面.

(2)当A=0 时,方程(2)成为By+Cz+D=0 ,法向量n=(0,B,C)垂直于x 轴,方程表示一个平行于x 轴的平面.

同理,方程Ax+Cz+D=0 和Ax+By+D=0 分别表示一个平行于y 轴和z 轴的平面.

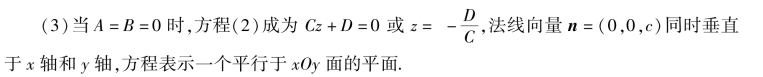(www.xing528.com)

同理,方程Ax+D=0 和By+D=0 分别表示一个平行于yOz 面和xOz 面的平面.

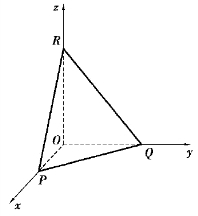
图7.17

例2　求通过x 轴和点(2,1,1)的平面的方程.

解　由于平面通过x 轴,则A=0,同时它必通过原点.又有D=0.因此,可设这平面的方程为

又因这平面通过点(2,1,1),故B+C=0 或C= -B.

以此代入所设方程,并除以B(B≠0),便得所求的平面方程为

例3　设一平面与x,y,z 轴的交点依次为P(a,0,0),Q(0,b,0),R(0,0,c)3 点,求这平面的方程(见图7.17,其中,a≠0,b≠0,c≠0).

解　设所求平面的方程为

因为P(a,0,0),Q(0,b,0),R(0,0,c)3 点都在这平面上,所以点P,Q,R 的坐标都满足方程(3),即

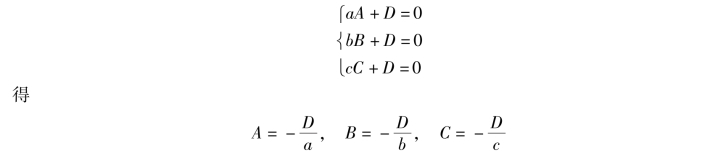
以此代入(3),并除以D(D≠0),得所求的平面方程为

方程(4)称为平面的截距式方程,而a,b,c 依次称为平面在x,y,z 轴上的截距.