高等数学下：向量积-高等数学及其应用（下）

在研究物体转动问题时,不但要考虑这物体所受的力,还要分析这些力所产生的力矩.为了引出向量积,先看下面的例子.

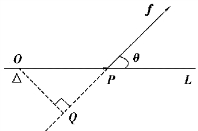
图7.14

这种由两个已知向量按上面的规则来确定另一个向量的情况,在其他力学和物理问题中也遇到,从而可抽象出两个向量的向量积概念.

定义7.5　由向量a 和b 可作出一个新的向量c,它满足下列两个条件:

(2)c 的方向垂直于a 与b 所决定的平面(即c 与a 和b 都垂直),c 的指向按右手规则确定.称向量c 为向量a 与b 的向量积(或叉积),记作a×b ,即

由向量积的定义可推得:

(1)a×a=0.

(2)对任意两个非零向量a,b,则a×b=0⇔a/ /b.

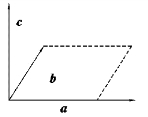
图7.15

向量积满足的运算规律:

(1)反交换律:b×a= -(a×b).

(2)分配律:(a+b) ×c=a×c+b×c.

(3)结合律:(λa) ×b=a×(λb) =λ(a×b)(λ 为数).(www.xing528.com)

向量积的坐标表达式:

设向量a=axi+ay j+azk ,向量b=bxi+by j+bzk.那么,按上述运算规律,得

因此

为了便于记忆,利用三阶行列式,上式可写为

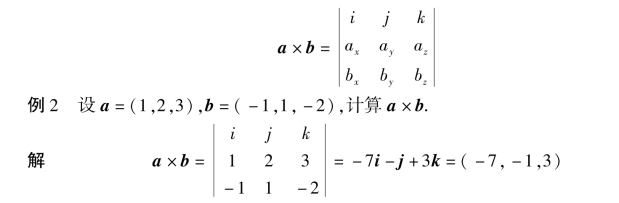
例3　△ABC 的顶点分别是A(1,2,3),B(2,3,5)和C(2,4,7) ,求△ABC 的面积.

解　根据向量积的定义及几何意义可知,△ABC 的面积

习题7.2

1.设a=3i-j-2k,b=i+2j-k,求:

(1)( -2a)·3b;　　　(2)a×2b;　　　(3)a,b

的夹角的余弦.

2.已知向量a=(3,5,-1),b=(2,1,3),c=(4,-1,3),计算:

(1)(a·b)·c-(a·c)·b;　　　(2)(a+b) ×(b+c).

3.已知三角形的3 个顶点坐标分别为A(0,1,-1),B(2,-1,4),C(4,1,5),求△ABC 的面积.

4.设向量a=(1,4,5),b=(1,1,2),求λ 使a+λb 垂直于a-λb.