设f(x)是以2π 为周期的函数,若f(x)可表示成三角级数,即
![]()
设f(x)在[ -π,π]上连续,级数逐项可积.由三角函数系的正交性,得
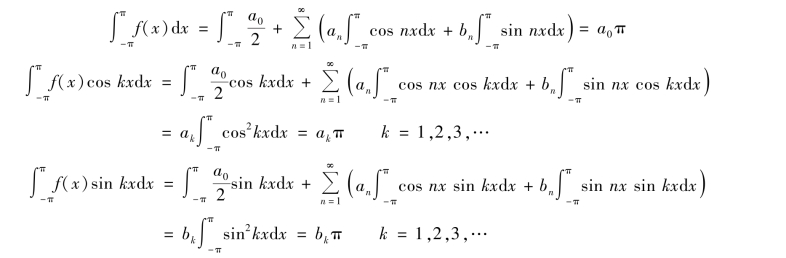
即三角级数的系数a0,an,bn 是由f(x)唯一确定
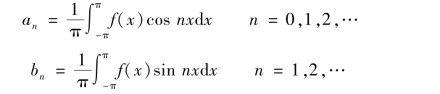
称其为f(x)的傅里叶系数,以此作为系数的三角级数称为傅里叶级数.
定理6.9[傅里叶级数的收敛性定理(狄利克雷充分条件)] 设=f(x)的周期为2π,且在一个周期[ -π,π]内,满足:
(1)连续或有有限个第一类的间断点;
(2)只有有限个极值点.
则f(x)展开成傅里叶级数.
在f(x)连续点,级数收敛于f(x);
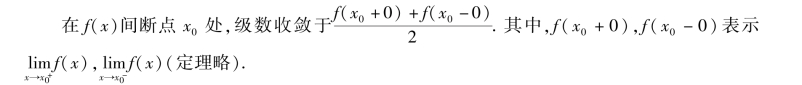
例1 设f(x)以2π 为周期,且在一个周期[ -π,π)内的表达式为
![]()
试将f(x)展开成傅里叶级数.
解 以2π 为周期的函数f(x)如图6.1 所示.
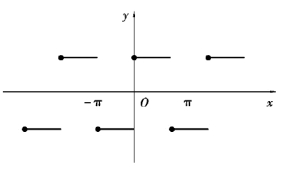
图6.1
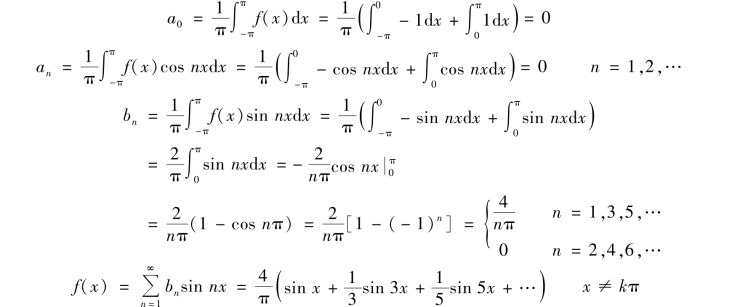
在间断点x=kπ 处,级数收敛于左右极限的平均值0,即
![]()
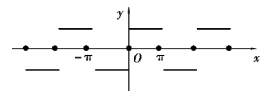
图6.2
f(x)的傅里叶级数的和函数的图如图6.2 所示.
定理6.10 设f(x)在[-π,π]上满足收敛定律的条件.(https://www.xing528.com)
若f(x)是[-π,π]上的奇函数,则傅里叶系数

若f(x)是[-π,π]上的偶函数,则傅里叶系数
注意 对在[0,π]上有定义的函数,根据要求可将其分别展开成正弦级数或余弦级数.
其方法如下:
(1)将f(x)奇延拓(或偶延拓)为[-π,π]上的奇函数(或偶函数).
(2)再将(1)中的函数以2π 为周期作周期延拓,然后展开.
(3)讨论傅里叶级数在[0,π]上的收敛性.
例2 设f(x) =π-x,x∈[0,π],分别将f(x)展开成:
(1)正弦级数; (2)余弦级数.
解 (1)将f(x)奇延拓后再周期延拓如图6.3 所示.
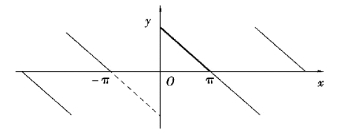
图6.3
因为f(x)奇延拓后为奇函数,则
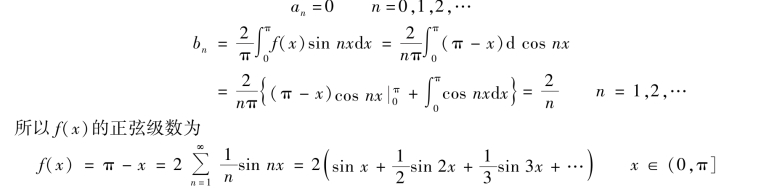
(2)将f(x)偶延拓后再周期延拓如图6.4 所示.
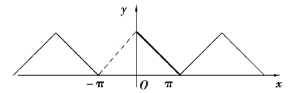
图6.4
因为f(x)偶延拓后为偶函数,则
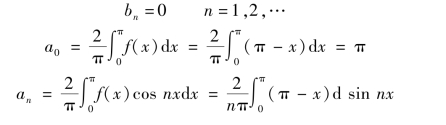
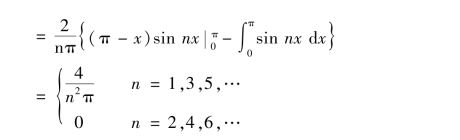
所以f(x)的余弦数为
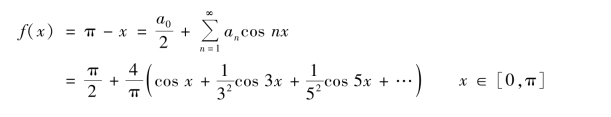
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




