一、内容小结
重积分和线面积分都是定积分的推广,即定义在区间上的一元函数和式的极限推广到定义在平面、空间区域或曲线曲面上的多元函数和式的极限.
(1)重积分和线面积分的思想和方法,实质上是与定积分是一致的,它们的定义结构相同,都是按“分割、近似、求和、取极限”的步骤构成的,也都有与定积分相类似的概念、性质.不同的是被积函数和积分区域.学习时,要注意它们的异同之处.
(2)在理解多元函数积分的概念、性质等理论基础上,应侧重于区分各类积分及其计算方法的掌握,其中尤以二重积分的计算最为重要,它是三重积分、曲线积分与曲面积分的基础.二重积分的计算下连定积分的计算,上连三重积分、线积分与面积分的计算,居于各种积分计算的中心环节.
(3)三重积分化为累次积分时,无论是采用“先一后二”还是“先二后单一”都需计算二重积分,而且三重积分在柱面坐标系中的计算实质上对应极坐标系中的二重积分的计算.
曲线积分与二重积分也密切相关,平面线积分计算的一条重要途径是通过格林公式把它转化为二重积分.而曲面积分的计算无论是对面积还是对坐标的面积分,都要化为二重积分去计算,而且二重积分本身其实就是一种特殊的曲面积分(积分域为平面区域).
(4)重积分有大量的实际问题作为背景,如立体的体积、曲面的面积、物体的质心与转动惯量等.对实际应用问题的处理方法依然可用“元素法”的思想与方法,即具有可加性的所求量的计算,只需分割整体,在微小的局部上求部分量的近似所求量元素,对元素求和即可得到所求量.
(5)二重积分计算的说明:
①二重积分与三重积分的计算是化积分为累次积分(定积分)来完成,化累次积分的关键在于确定积分的次序及积分上下限,这是学习的重点.
重积分计算,首先画一积分区域的草图是有必要的,根据积分区域的形状和被积函数的具体情况,选定一种计算较方便的积分次序,并确定积分上下限.
②二重积分化为二次积分可分为直角坐标系中和极坐标系中两种情况.
当积分区域为矩形、三角形,边界为直线及曲线围成时,依据区域为X 型或Y 型,在直角坐标系中化积分为二次积分.面积元素dσ 用dxdy 替代.
(6)三重积分计算的说明:
①三重积分计算,可依据积分区域Ω 的构成,确定不同坐标系中计算积分.
当积分区域为长方体、四面体及边界由平面所围的其他形状时,采用直角坐标系下计算三重积分;
当积分区域为柱体、锥体及由柱面、锥面、旋转面所围的其他形状时,采用柱面坐标系下计算三重积分;
当积分区域为球体、或球体的部分与锥体所围的其他形状时,采用球面坐标系下计算三重积分.
②投影法确定三重积分的积分次序及积分上下限,常用“先一后二”的次序化三次积分计算积分.先定积分、后二重积分的具体做法是:
a.将积分区域Ω 投影到坐标面上的平面区域D;
b.根据D 的情况,决定二重积分为直角坐标系下或极坐标系下的二次积分.
即对应三重积分在直角坐标系中或柱面坐标系中化积分为三次积分计算.其中,柱面坐标系中被积函数和体积元素分别化为
③如果积分区域Ω 是球体或者由球面及锥面围成的立体,被积函数中含有x2 +y2 +z2,用球面坐标较方便.三重积分转化为球面坐标系中的三次积分时,被积函数和体积元素分别转化为
④若被积函数只与一个变量z 有关,过z 点作垂直于Oz 轴的平面截Ω,截面为Dz 面积较易求得.可将三重积分化为“先二后一”(先二重积分,后定积分)的三次积分.
二重积分与三重积分在直角坐标系、极坐标系、柱面坐标系中的计算表,供对照学习.
(7)线面积分计算的说明:
①线积分的计算.
a.曲线C 的方程为x=x(t),y=y(t),α≤t≤β,那么
b.曲线C 的方程为x=x(t),y=y(t),z=z(t),α≤t≤β,那么
积分的上下限应分别对应于终点和起点,不可弄错.这与曲线C 的方向有关.
②面积分的计算.
a.曲面K 的方程为z=z(x,y),那么
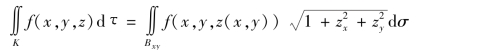
其中,B 为K 在坐标平面xOy 上的投影域.
同样,当曲面K 的方程为x=x(y,z)或y=y(z,x),那么
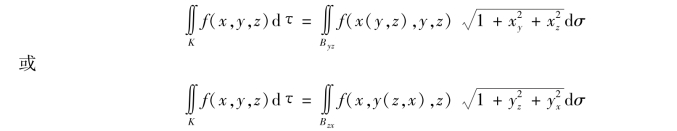(www.xing528.com)
其中,Byz与Bzx分别为K 在yOz 与zOx 上的投影域.
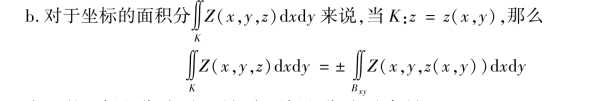
在K 的上侧积分时,取正号;在下侧积分时,取负号.
当K:x=x(y,z)或y=y(z,x),那么类似地可得
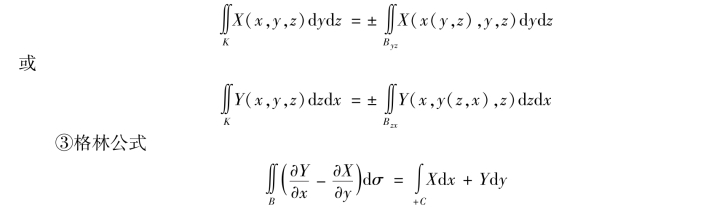
二、教学要求
(1)理解二重积分、三重积分的概念;了解重积分的性质.
(2)掌握在直角坐标系中和极坐标系中二重积分的计算法(二次积分的次序选择,积分上下限的确定).
(3)掌握三重积分在直角坐标系中和柱坐标系中“先一后二”的计算法;知道“先二后一”及球面坐标系中计算三重积分的方法.
(4)了解重积分在几何和物理中的应用,会利用公式解决一些简单问题的计算.
(5)理解曲线积分和曲面积分的概念、性质,掌握它们的计算法.
(6)理解格林公式.
(7)理解曲线积分与路径无关的条件.
本章的重点:二重积分的计算方法(二次积分次序选择,积分上下限的确定);三重积分“先一后二”的计算法;线面积分的计算方法.
本章的难点:积分次序选择;积分上下限的确定;格林公式的应用.
二重积分与三重积分计算表见表9.1.
表9.1 二重积分与三重积分计算表
三、本章练习题
(一) 选择题
(二) 填空题
(三) 计算题
(五) 证明题
(六) 应用题
1.计算由曲面z = x2 + y2,3 个坐标面及平面x + y = 1 所围成立体的体积.
2.求两个圆柱面x2 + y2 = a2 和x2 + z2 = a2 所围成立体的表面积A.
3.求高为H、底半径为R 的圆锥体的形心.
黄金分割的自然与美丽
第9 章参考答案
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
