高等数学应用：二阶常非齐次线性微分方程

二阶常系数非齐次线性微分方程

对应的齐次微分方程

定理5.2(通解结构定理)　设y*是微分方程(4)的一个特解,Y=C1y1 +C2y2 是对应的齐次方程(5)的通解,则二阶常系数非齐次线性微分方程的通解为

由上式可知,二阶常系数非齐次线性微分方程的通解结构为:非齐次方程(4)的一个特解与对应的齐次方程(5)的通解之和,即

将y=y* +Y 代入式(4),则

的特解(用上面的代入的方法,即可证得).

本节只介绍右端项f(x)常见的几种情形,下面分别加以讨论.

1.右端项为f(x) =Pn(x)eαx

由于方程中y″,y′及y 的系数是常数,可推测它的特解也是多项式与eαx乘积的形式. 因此,设特解为y* =Qn(x)eαx,其中Qn(x)为待定多项式,则

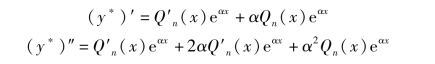
代入式(4),并消去eαx,整理得

等式两边都是x 的多项式,用待定系数法来确定Qn(x).

(1)当α2 +pα+q≠0,即α 不是特征方程的根时,应设多项式Qn(x)与Pn(x)同为x 的n次多项式.其系数可由等式两边x 的同次幂的系数对应相等来确定.

(2)当α2 +pα+q=0,而2α+p≠0,即α 是特征方程的单根时,式(6)为

应设y* =xQn(x)eαx,即将y*中多项式的次数提高一次.可用同样的方法比较系数确定Qn(x).

(3)当α2 +pα+q=0,且2α +p =0,即α 是特征方程的重根时,应设y* =x2Qn(x)eαx,然后比较系数确定Qn(x).

例4　求微分方程y″-y=2x2 -3 的通解.

解　方程对应的齐次方程为y″-y=0,其特征方程r2 -1 =0 的根为r1 = -1,r2 =1.因此,对应齐次方程的通解为

方程的右端项f(x) =2x2 -3 属于Pn(x)eαx型(n =2,α =0)而α =0 不是特征方程的根.因此,设特解为

将(y*)′=2Ax+B, (y*)″=2A 代入原方程,则

比较方程两边x 的同次幂的系数,有

即C= -7.

原方程的特解为

故原方程的通解为

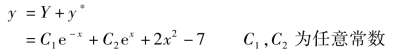
例5　求微分方程y″+2y′-3y=ex 的通解.

解　方程对应的齐次方程为y″+2y′-3y =0,其特征方程r2 +2r -3 =0 的根为r1 = -3,r2 =1.因此,对应齐次方程的通解为

方程的右端项f(x) =ex 属于Pn(x)eαx 型(其中,n =0,α =1),而α =1 是特征方程的单根.因此,设特解为

将(y*)′=(Ax+A)ex, (y*)″=(Ax+2A)ex 代入原方程,则

整理有

(www.xing528.com)

故原方程的通解为

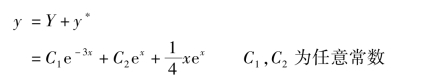
例6　求微分方程y″-4y′+4y=(2x+1)e2x的通解.

解　方程对应的齐次方程为y″-4y′+4y=0,其特征方程r2 -4r +4 =0 的根为r1 =r2 =2(重根).因此,对应齐次方程的通解为

方程的右端项f(x) =(2x+1)e2x属于Pn(x)eαx型(其中,n =1,α =2).而α =2 是特征方程的重根.因此,设特解为

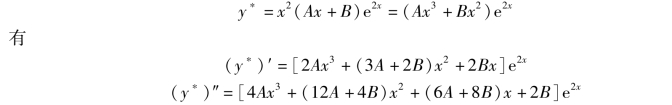
将它们代入原方程并整理,得

即6Ax+2B=2x+1.

原方程的特解为

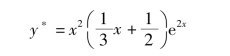
故原方程的通解为

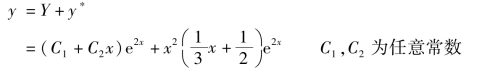
2.右端项为f(x) =eαx[Pl(x)cos βx+Pm(x)sin βx]

不加证明地给出以下结论:方程

的特解具有形式

其中,Qn(x),Rn(x)是n 次多项式,n=max {l,m}.

当α±βi 不是特征方程的根时,k=0;当α±βi 是特征方程的根时,k=1.

例7　求微分方程y″+4y=x cos x 的通解.

解　方程对应的齐次方程为y″+4y=0,其特征方程r2 +4 =0 的根为r1,2 = ±2i.因此,对应齐次方程的通解为

方程的右端项f(x) =x cos x 属于eαx[Pl(x)cos βx+Pm(x)sin βx]型(其中,α=0,β=1) ,而α±iβ= ±i 不是特征方程的根.因此,设特解为

将y*″,y*代入原方程整理,则

比较系数,得

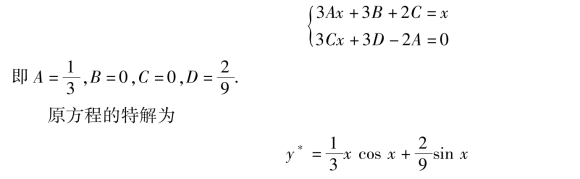
故原方程的通解为

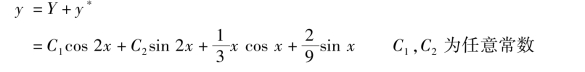
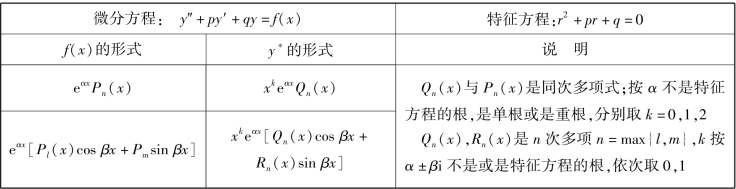
根据二阶常系数非齐次线性方程右端项f(x)的形式及所对应的齐次方程的特征方程根的情况,用待定系数法确定方程特解的形式,汇总成表5.2,以便于使用.

表5.2　二阶常系数非齐次线性微分方程的特解形式表

习题5.4

1.求下列微分方程的通解:

(1)y″-4y′+3y=0;　　　　　　　　　　　(2)y″-y′-6y=0;

(3)y″-6y′+9y=0;(4)y″+2y′+y=0;

(5)y″+4y=0;(6)y″-4y′+5y=0.

2.求下列非齐次线性微分方程的通解:

(1)2y″+y′-y=2ex;(2)y″-2y′-3y=2x+1;

(3)y″-6y′+9y=(x+1)e3x;(4)y″+4y=8 sin 2x.

【验证性实验】