红兴隆分局粮食增产潜力预测：实现成果

（一）红兴隆分局粮食增产影响因子变化趋势分析预测

1.粮食播种面积预测

根据红兴隆分局1992～2006 年的耕地面积资料（表8-17）绘制耕地面积变化曲线，见图8-13。

表8-171992～2006年红兴隆分局耕地面积　单位：万hm2

注 由于在所收集的红兴隆分局耕地面积资料中，缺失1994年的数据，所以表中1994年数据为三次样条插值法插值结果。表中其余年份数据来源于红兴隆分局历年《经济与社会发展统计资料》。

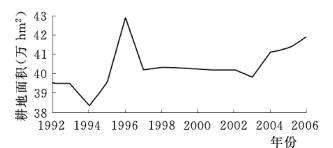
图8-13　红兴隆分局耕地面积变化曲线（1992～2006 年）

由表8-17和图8-13 可以看出，红兴隆分局耕地面积的变化大致经历了三个阶段。第一阶段：1992～1996 年，耕地面积波动式增长阶段。1992～1994 年，耕地面积逐年减少，1994年，耕地面积降至历史最低值38.32万hm2，年平均耕地损失率为1.49%。1995～1996 年，耕地面积迅速增加，1996 年，耕地面积达到历史最高值42.91 万hm2，年平均耕地增长率为5.99%。第二阶段：1997～2003 年，耕地面积缓慢减少阶段。该阶段由于工业企业和小城镇建设的迅速发展，使得耕地面积逐年减少，年平均耕地损失率为1.49%。第三阶段：2004～2006 年，耕地面积持续增长阶段。该阶段耕地面积逐年增加，年平均耕地增长率为1.76%。目前我国耕地资源呈逐年下降的趋势，而红兴隆分局近三年耕地面积不降反升，这主要是由于开发利用后备耕地资源所导致的。

考虑到我国社会主义新农村建设过程中建设占地以及耕地保护政策执行力度逐渐加强等因素的影响，2007～2010年、2011～2020年、2021～2030 年红兴隆分局年平均耕地损失率分别按0.5%、0.3%、0.1%粗略估计。2006 年，红兴隆分局后备耕地资源为6.76万hm2，预计到2010 年、2020 年、2030 年，后备耕地资源开发率将分别达到10%、30%和50%。红兴隆分局复种指数为1。若粮食播种比例按红兴隆分局多年平均值85%计，则可以按照公式：粮食播种面积＝耕地面积×复种指数×粮播比例[36]对红兴隆分局2010年、2020年、2030年粮食播种面积进行预测，见表8-18。

2.粮食单产分析预测

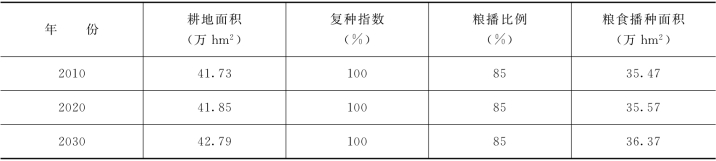
根据1995～2006 年红兴隆分局粮食单产资料（表8-12）建立红兴隆分局粮食单产乘幂型回归模型如下：

表8-18　红兴隆分局粮食播种面积分析预测

式中：y 为粮食单产，kg∕hm2；x 为年份。

采用式（8-19）进行计算，得到2010 年、2020 年、2030 年红兴隆分局粮食单产预测值：

3.有效灌溉面积分析预测

根据1992～2006 年红兴隆分局有效灌溉面积资料（表8-13）建立红兴隆分局有效灌溉面积乘幂型回归模型如下：

式中：y 为有效灌溉面积，万hm2；x 为年份。

采用式（8-20）进行计算，得到2010 年、2020 年、2030 年红兴隆分局有效灌溉面积预测值：

4.化肥施用量分析预测

根据1992～2006 年红兴隆分局化肥施用量资料（表8-14）建立红兴隆分局化肥施用量线性回归模型如下：

式中：y 为化肥施用量，万t；x 为年份。

采用式（8-21）进行计算，得到2010 年、2020 年、2030 年红兴隆分局化肥施用量预测值：

2006年，红兴隆分局化肥施用量达到12.53 万t，根据上述预测值进行计算，2007～2010年、2011～2020 年、2021～2030 年化肥施用量年平均增长率分别为3.51%、3.14%、2.39%，增长率逐渐降低，因此上述预测结果是比较合理的。

5.农机总动力分析预测

根据1992～2006 年红兴隆分局农机总动力资料（表8-15）建立红兴隆分局农机总动力线性回归模型如下：

式中：y 为有效灌溉面积，万hm2；x 为年份。

采用式（8-22）进行计算，得到2010 年、2020 年、2030 年红兴隆分局农机总动力预测值：

6.农田旱涝灾害成灾面积分析预测

2000～2006 年，红兴隆分局农田旱涝灾害平均成灾面积为8.98 万hm2，占平均耕地面积的22%。随着水利建设资金不断的增加，可以预计，红兴隆分局抵抗农业旱涝灾害的能力必然会逐步加强。若到2010年、2020年、2030年，农田旱涝灾害成灾面积占耕地面积的比例分别按16%、14%、12%计，则粗略估算，到2010 年、2020 年、2030 年，红兴隆分局农田旱涝灾害成灾面积分别控制在6.68万hm2、5.86 万hm2、5.13 万hm2。

（二）偏最小二乘回归模型在红兴隆分局中长期粮食总产量预测中的应用

前面所建的红兴隆分局粮食总产量回归模型虽然拟合精度满足要求，但1994 年、1995 年预测值的相对误差分别达到43.16%和32.51%，这主要是由于主成分分析法虽然克服了回归建模中的多重相关性问题，但在分析的第一步就完全撇开了因变量，单独针对自变量的集合进行主成分提取，这样所得到的前几个主成分虽然对自变量系统具有很强的概括能力，但对因变量却缺乏合理的解释，因此导致模型拟合结果令人不满意。

当变量间存在较严重的多重相关性时，传统的多元回归分析、主成分分析等方法建模效果往往不够理想。为了很好地解决变量间的多重相关性问题，提高模型的精度、稳健性和实用性，可以采用偏最小二乘回归（partial least－squares regression，简称PLSR）模型。偏最小二乘回归是一种多元统计分析的新方法，由伍德（S.Wold）和阿巴诺（C.Albano）等人于1983 年首次提出。它集多元线性回归分析、典型相关分析和主成分分析的基本功能为一体，将建模预测类型数据分析方法与非模型式的数据认识性方法有机结合起来[37～40]，即：

偏最小二乘回归≈多元线性回归分析＋典型相关分析＋主成分分析

1.偏最小二乘回归模型建模思路与算法

最后，定义交叉有效性为：

（3）偏最小二乘回归简化算法。偏最小二乘回归简化算法计算过程[37，40，41，43，44]如下：

1）标准化处理。记F0为因变量Y 的标准化矩阵，E0为自变量集合X 的标准化矩阵，则：

2）成分提取。

3）推求偏最小二乘回归模型。根据已经提取的m个成分t1、t2、…、tm，实施F0对t1、t2、…、tm的回归，得：

2.实例分析

（1）资料来源。选择红兴隆分局粮食总产量（y）作为因变量，选择与红兴隆分局粮食增产密切相关的粮食播种面积（x1）、粮食单产（x2）、有效灌溉面积（x3）、化肥施用量（x4）、农机总动力（x5）和农田旱涝灾害成灾面积（x6）六个影响因子作为自变量。采用1992～2003 年资料建模，2004～2006 年资料留作预留检验。

（2）多重相关性诊断。采用方差膨胀因子对各自变量之间是否存在多重相关性进行诊断。自变量xj的方差膨胀因子记为（VIF）j，其表达式为

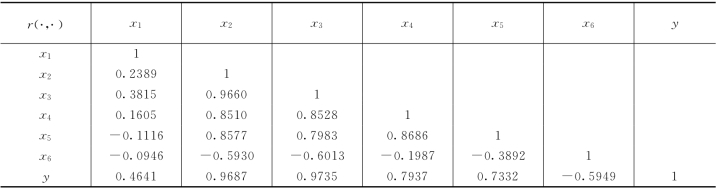
表8-19　自变量、因变量之间的相关系数矩阵(www.xing528.com)

因此，变量间存在多重相关性。

（3）建立粮食总产量偏最小二乘回归模型。首先将因变量（粮食总产量）序列yi（i＝1，2，…，12）、自变量（粮食增产各影响因子）序列xij（i＝1，2，…，12；j＝1，2，…，6）进行标准化处理，得到因变量与自变量的标准化序列F0与E0j。然后根据前述的建模简化算法采用MATLAB7.0软件编程计算，过程如下：

1）提取第一成分。

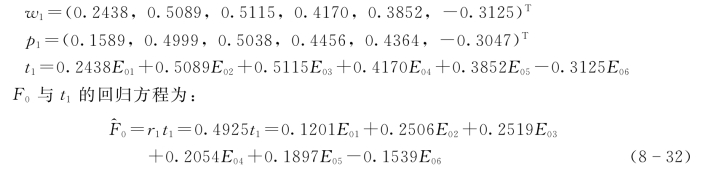
回归方程的复相关系数R＝0.9682，F＝164.92。

2）提取第二成分。

回归方程的复相关系数R＝0.9868，F＝185.34。

3）提取第三成分。

4）建立偏最小二乘回归方程。

上述计算结果表明，提取2个成分就可以满足要求。因此，标准化变量回归方程为：

将标准化变量回归方程变换为原始变量回归方程：

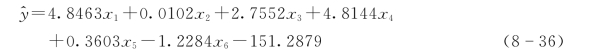
（4）模型辅助分析。

1）精度分析。前述分析中共提取了2个成分，这两个成分与原自变量x1～x6以及因变量y 的相关系数平方见表8-20。

表8-20　r2（th，xj）与r2（th，y）计算结果

表8-21　累计解释能力

由表8-21 可以看出，t1、t2对全部自变量X 的累计解释能力为83.73%，而对因变量y 的累计解释能力为97.38%。t1、t2对各自变量xj的累计解释能力中，除了对x6的累计解释能力较小外，对其余自变量的累计解释能力均在80%以上，说明t1、t2能很好地解释自变量和因变量。

2）自变量对因变量的解释作用。在偏最小二乘回归分析中，利用变量投影重要性指标VIPj（variableimportanceinprojection）来测度自变量对因变量的解释能力。其表达式为[37，42，45]：

对于VIPj很大（＞1）的xj，它在解释y 时就有更加重要的作用。

根据式（8-38）计算各变量的VIPj值，绘制VIPj直方图，见图8-14。

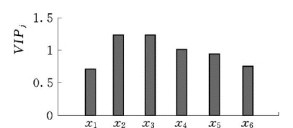
图8-14　各变量VIPj直方图

由图8-14可以看出，各变量对红兴隆分局粮食总产量解释能力排序为：x3＞x2＞x4＞x5＞x6＞x1，其中粮食单产（x2）、有效灌溉面积（x3）、化肥施用量（x4）的VIPj值大于1，说明它们对y 的解释能力强于其他粮食增产影响因子，对解释红兴隆分局粮食总产量的变化起着重要作用。

3）偏最小二乘回归的成分。分别绘制t1∕u1（u1＝F0∕r1）平面图、t2∕u1平面图，见图8-15 和图8-16。从图8-15 可以看出，t1与u1之间存在明显的线性关系。从图8-16可以看出，t2与u1的线性关系明显减弱，但线性趋势还是存在的。

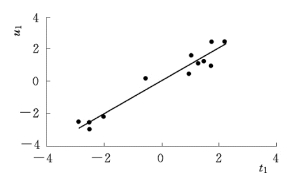
图8-15　t1∕u1平面图

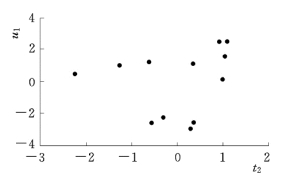
图8-16　t2∕u1平面图

4）对成分的解释。计算所提取成分th与xj和y 的相关系数，根据相关程度来解释th的物理含义。本例的相关系数、权重以及回归系数的计算结果见表8-22。

表8-22　相关系数、权重以及回归系数的计算结果

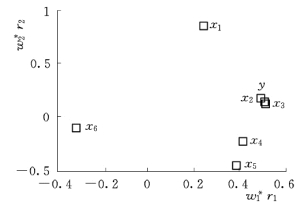
图8-17　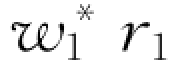∕ 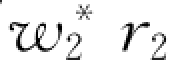平面图

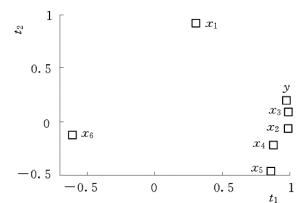
图8-18　相关系数图

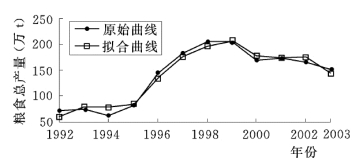
图8-19　红兴隆分局粮食总产量偏最小二乘回归模型拟合曲线（1992～2003 年）

（5）模型拟合。采用建立的红兴隆分局粮食总产量偏最小二乘回归模型对1992～2003年红兴隆分局粮食总产量进行拟合，见图8-19。从图8-19 可以看出，所建粮食总产量偏最小二乘回归模型拟合效果良好。

（6）模型精度检验。采用所建粮食总产量偏最小二乘回归模型的拟合数据进行拟合效果检验。经过计算，拟合效果评价指标后验差比值C＝0.0791，小误差频率p＝1，拟合准确率为91.67% （相对误差e＜20%为合格），其中，C、p 均达到1 级标准，拟合准确率达到Ⅱ级标准。

采用未参加建模的红兴隆分局2004～2006 年粮食总产量及6 个影响因子的原始数据进行后验预测检验，见表8-23。

表8-23　红兴隆分局粮食总产量最小二乘回归模型后验预测误差（2004～2006年）

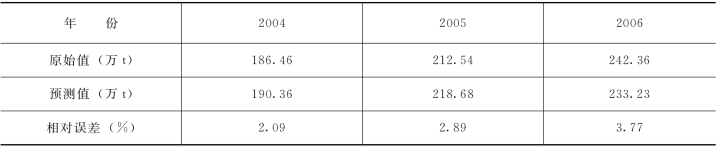
经过计算，预测检验合格率为100% （相对误差e＜20%为合格），达到1 级标准。因此，所建的红兴隆分局粮食总产量偏最小二乘回归模型可靠性和预测精度较高，可用于预测红兴隆分局未来粮食总产量。

（7）回归模型预测。将前述粮食播种面积（x1）、粮食单产（x2）、有效灌溉面积（x3）、化肥施用量（x4）、农机总动力（x5）和农田旱涝灾害成灾面积（x6）2010 年、2020年、2030年的预测值代入式（8-36），得到2010 年、2020 年、2030 年红兴隆分局粮食总产量的预测值：