基于RAGA的PPC模型在水稻优化灌溉制度的应用

（一）分蘖——幼穗分化阶段优化灌溉制度的PPC模型

将各处理的试验调查数据作为分析的状态变量，见表5-9、表5-10。[11]

选定父代初始种群规模为n＝400，交叉概率pc＝0.80，变异概率pm＝0.80，优秀个体数目选定为20个，α＝0.05，加速次数为20，得出最大投影指标值为0.6578，最佳投影方向a*＝（0.3203，0.0162，0.3779，0.3306，0.3773，0.2843，0.2402，0.3632，0.3795，0.2970），将a*代入式（3-10）后即得各种灌溉模式的投影值z*（j）＝（0.1615，2.1905，2.8797，0.6244）。将z*（j）从大到小排列，可得各种灌溉模式的优劣排序，即C模式＞B模式＞D模式＞A模式，可见C灌溉模式最好，其次是B模式，D模式更次之，最后是A模式，见图5-17。

表5-9　分蘖——幼穗分化期的状态变量xi[11]

表5-10　分蘖——幼穗分化期的状态变量xi[11]

（二）灌浆——成熟阶段水稻优化灌溉制度的PPC模型(www.xing528.com)

首先将数据归一化处理后得：

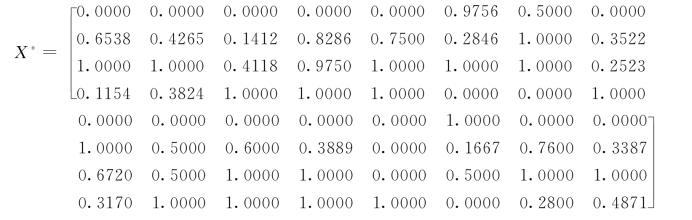
同样选择n＝400，交叉概率pc＝0.80，变异概率pm＝0.80，优秀个体数目选定为20个，α＝0.05，加速次数为20，得出最大投影指标值为0.8934，最佳投影方向a*＝（0.3096，0.3297，0.1279，0.2937，0.2785，0.1021，0.3028，0.1250，0.2664，0.1727，0.3041，0.2983，0.1217，0.0373，0.3413，0.2874），将a*代入式（3-10）后即得各种灌溉模式的投影值z*（j）＝（0.2883，2.2034，3.2084，2.2037）。将z*（j）从大到小排列，可得各种灌溉模式的优劣排序，即C模式＞D模式＞B模式＞A模式，可见C灌溉模式最好，其次是D模式，B模式更次之，最后是A模式。见图5-18。

图5-17　投影值z*（j）散布图

图5-18　投影值z*（j）散布图