由于门限自回归模型是分区间的AR模型，因此在建模中只需沿用AR建模的参数估计方法和模型检验准则，并不存在实质性的困难。目前应用较多的是模型参数估计的最小二乘法与模型适用性检验的AIC 准则。与AR建模不同的是建立SETAR模型的难点并不在于参数估计和模型检验，而在于确定门限区间个数l、门限值r1，r2，…，rl－1和延迟步数d。从理论上讲，这是一个对l，r1，r2，…，rl－1和d 的多维寻优问题。若采用AIC准则作为模型定阶（确定各门限区间的模型阶数n1，n2，…，nl）和确定l，r1，r2，…，rl－1和d 这些参数的目标函数，则AIC 应是所有这2l＋1 个参数的函数，即：
适用的SETAR模型的AIC 值应是上式所示的多维空间中超曲面的极小点。
本节介绍将H.Tong方法和D.D.C方法结合共同建立SETAR模型。
（一）D.D.C方法求点值图[10]
D.D.C方法是由吴今培等提出。其思路是在建模中采用点值图（DotFigure）确定门限区间的个数l 和门限值r1，r2，…，rl－1的搜索范围，采用迭代法（Duplication Meth_od）估计模型参数，采用互证法（Cross_Validation Method）确定延迟步数d，简记为D.D.C。其中的迭代法就是对AR模型参数的矩阵递推最小二乘法。建模第一步就是采用点值图法确定门限区间的个数l 和门限值r1，r2，…，rl－1的搜索范围。
点值图法常称为条件数学期望估计法。
归纳起来，采用点值图法确定l 和r1，r2，…，rl－1的搜索范围的步骤为：
（4）采用线性回归方法判断点值图中的点是否可以用直线来拟合，根据直线段的数目确定l 值，并在各直线段的转折处确定rj（j＝1，2，3，…，l－1）的搜索范围。
（二）H.TonG方法求最优延迟步数d、rj和φj（i ）[11]
H.Tong方法是一种对d，l，rj（j＝1，2，3，…，l－1）层层嵌套一维寻优的方法。其基本思路是：首先固定一组d，l，rj（j＝1，2，3，…，l－1），分别在各区间内建立AR模型，按AIC 准则分别确定每一区间的适用模型，从而得到一个SETAR模型；然后分别改变d，l，rj（j＝1，2，3，…，l－1）的值，同样再分区间建立AR 模型以得到SETAR模型，比较各种d，l，rj（j＝1，2，3，…，l－1）情况下所建SETAR 模型的AIC值，确定其中AIC 值最小的模型为适用模型。由于门限区间已经由点值图法确定了。因此可以减少一层嵌套，即l 为已知。具体步骤如下：
（1）令延迟步数d＝1 和点值图法确定的门限值rj（j＝1，2，3，…，l－1）的搜索区间，将时间序列｛x （t－ d ）｝（t＝d＋1，d＋2，…，N）按其属于哪一个区间加以分段，共分成l 个子序列：
（2）在各个门限区间建立AR模型。通过自相关分析，确定模型形式，再通过偏相关分析，初步确定模型阶数nj。
若有p 阶相关系数均显著于独立序列，则原随机序列为一相依序列，可选用AR（p）模型。(www.xing528.com)
阶数p 确定主要方法是对偏相关系数进行统计分析。偏相关系数φ（k ）可用递推算法求得：
建立AR（n1）—n1＝p 模型：
同理，分别建立各门限区间的AR模型。然后对各个模型用AIC 准则检验判别：
显然，在此时给定d，l，rj（j＝1，2，3，…，l－1）的情况下，AIC 的值仅是模型阶数nj的函数，AIC 最小时的模型即为各区间内的适用模型，即各区间内适用模型的AIC 值为：
M 为模型最高阶数。
（3）将各门限区间内的适用ARj（nj）（j ＝1，2，3，…，l）模型组合起来得到SETAR模型，该模型的AIC 值为各区间模型AIC 值之和，即：
由于此时是在d，l，rj（j＝1，2，3，…，l－1）这l＋1 个参数固定情况下所得到的SETAR模型和AIC 值，故式（5-26）所示的AIC 值是这l＋1 个参数的函数；
（4）仍然固定d，l，采用黄金分割法（或加速遗传算法RAGA）在给定搜索范围内对门限值rj（j＝1，2，3，…，l－1）进行寻优。重复上述步骤，按式（5-27）求出AIC值，确定其中AIC 值达最小时的一组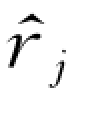
（j＝1，2，3，…l－1）为给定d，l 时的最优门限值，即门限值寻优的目标函数为：
至此，参数寻优过程全部结束，建立起SETAR（l，d，n1，n2）模型。
（三）SETAR模型的预测（最佳预报）[11，12]
则门限自回归模型的最佳预报公式为：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
