三江平原井灌区水资源利用与可持续发展研究

作为一种水资源开发利用策略，目前，世界上许多国家都在致力于地下水人工补给的应用和研究。地下水人工补给方法有多种，各个地区地下水人工补给方法的选择受到当地水源条件、气候植被条件、地形地貌条件、包气带条件和充水岩层条件等因素的制约[36]。本节尝试以红兴隆分局为例，采用改进AHP选择红兴隆分局最佳地下水人工补给方法，为将来地下水人工补给实践以及地下水资源的可持续利用提供依据。

（一）层次分析法基本原理

层次分析法（AHP）是由美国运筹学家T.S.Satty教授于20世纪70年代提出，它是一种处理多准则、多目标复杂问题的简单决策工具[37]。经过多年的发展，层次分析法已经在能源系统分析、城镇规划、经济管理、科技成果评价以及工程技术等众多领域得到了广泛应用。层次分析法的基本原理是：把复杂问题分解成各个组成要素，将这些要素按照支配关系分组形成递阶层次结构（即目标层、准则层、方案层等层次），在此基础上对各层次中诸因素进行定性和定量分析，最后综合决策者的判断确定各决策方案相对重要性的总排序[38]。

（二）层次分析法基本步骤

采用AHP法进行决策时，一般包括以下四个主要步骤[39，40]。

1.构造层次结构模型

根据所研究问题的性质的决策目标，分析复杂问题各组成要素之间的关系，建立递阶层次结构。

2.构造判断矩阵

采用问卷调查的方法，要求受调查者按照1－9 标度法[39]，对同一层次中各因素相对于上一层次中某一准则的重要性进行两两比较，从而可以构造判断矩阵如下：

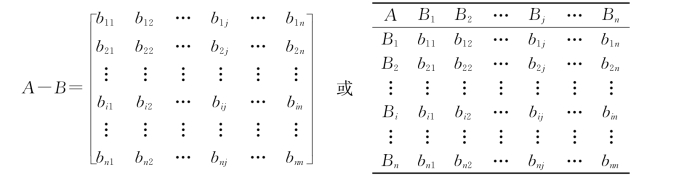
式中：bij为Bi与Bj两两比较，对A而言Bi的相对重要性数值。

3.建立权重集

（1）层次单排序。根据判断矩阵推算各层次中诸因素相对于上一层问题的相对重要性系数（也称为权重）即为层次单排序。例如根据判断矩阵A－B 推算Bi（i＝1，2，…，n）相对于上一层A的相对重要性系数，记为WBi。WBi可以采用方根法[41]求解：

1）计算判断矩阵中每一行元素的乘积，即：

（2）层次总排序。根据层次单排序的计算结果推算最底层各因素相对于最顶层问题的相对重要性系数即为层次总排序。例如对于从上至下划分为A、B、C 三层的层次结构，层次总排序的组合权重Wp计算公式为[42]：

式中：m为最底层C 中的因素数量。

4.一致性检验

为了评价层次排序的有效性，还必须对判断矩阵的评价结果进行一致性检验。可以采用T.L.Seaty提出的随机一致性比值C×R 的概念进行一致性检验，C×R 的计算公式为[39，41]：

式中：R×I 为随机性指标，与判断矩阵的阶数n 有关，具体取值可参考文献[39]、[41]；C×I 为一致性指标，其计算公式为：

式中：λmax为判断矩阵的最大特征根，其计算公式为：

式中：B 为已知判断矩阵；n为矩阵B 的阶数。

若经过计算，满足C×R＜0.1，则说明判断矩阵B符合一致性要求，层次排序有效。一般来讲，当层次单排序满足一致性要求后，层次总排序的一致性也会得到满足。为了把握起见，也可以对总排序的有效性进行检验，其计算公式为：

若经过计算，式（4-43）满足C×R＜0.1，说明层次总排序符合一致性要求，层次排序有效。

（三）层次分析法的改进

由于传统层次分析法采用1－9 标度法构造判断矩阵，有可能使得各因素间权重值差距过大（最大可达9 倍），某些因素在系统中的作用得不到充分体现。因此本节采用修正系数法对传统层次分析法进行改进，具体方法如下[43]：

（四）基于改进AHP的红兴隆分局最佳地下水人工补给方法研究

黑龙江省农垦红兴隆分局位于黑龙江省东部——三江平原中部，地跨佳木斯、双鸭山、七台河等四市七县，总面积为0.88万km2，其中耕地面积为40万hm2。红兴隆分局下辖12个国营农场，机械化程度达到95%以上，盛产小麦、大麦、大豆、水稻、玉米，是国家重要的商品粮生产基地。随着粮食作物种植结构的调整、寒地水稻栽培新技术的推广应用以及水稻本身所具有的经济效益，垦区水稻的种植面积迅速增加。红兴隆分局的水稻种植面积由1996 年的7.7万hm2激增到2005年的17.1万hm2 （其中66%以上为井灌水田）。随着水田面积的迅速增加，红兴隆分局的地下水位普遍下降，平均年降幅为0.5～1.0m∕a，局部地区形成暂时性的降落漏斗。地下水位持续下降已经严重地破坏了当地地下水资源的供需平衡。按此趋势发展下去，必然会对当地的工农业生产和居民用水产生严重威胁。因此，结合国内外地下水修复工作的经验，为了实现区域农业的可持续发展，应加强地下水人工补给研究。本节以红兴隆分局为例，采用改进AHP对该地区的地下水人工补给方法进行评价和选择。

1.地下水人工补给方法识别(www.xing528.com)

在参考大量国内外文献并对有丰富地下水工作经验的水利专家进行访谈的基础上，对地下水人工补给方法进行识别，见前述。

2.构造地下水人工补给方法评价模型

按照目标层、准则层、方案层几个层次将已经识别出的地下水人工补给方法层次化，从而构成黑龙江省农垦红兴隆分局地下水人工补给方法评价模型，见图4-16。

3.构造判断矩阵

（1）调研及统计方法。采用问卷调查方法，要求受调查者[黑龙江省水利厅、农垦总局水务局决策者，红兴隆分局（含下属12 个农场）水务局技术人员，黑龙江省科研、设计院所水利专家及高校水利专家]根据经验对已经识别出的各种地下水人工补给方法的重要性作出评价，在问卷调研及修改阶段，受调查人员普遍反映问卷中所列举的地下水人工补给方法还是相当全面的。

图4-16　红兴隆分局地下水人工补给方法评价模型

本次调查总共发放问卷270份，回收率达到37.8%，见表4-11。受调查人员的职称结构及从业年限情况见表4-12 和图4-17。表4-12 和图4-17 中的数据说明受调查者具有相当丰富的从事地下水工作的经验，对三江平原特别是井灌水稻区的地下水状况有相当清晰的了解，这确保了本次问卷调查最终结果的可靠性。

表4-11　问卷回收率

表4-12　受调查人员的职称结构及从业年限

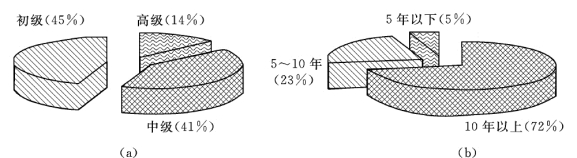
图4-17　受调查人员的职称结构及从业年限状况

（a）职称结构；（b）从业年限比例

（2）判断矩阵。根据问卷调查的结果，对专家意见汇总后进行加权平均。根据专家意见，第二层B中各因素对应于第一层A的重要性差距不应超过3 倍，第三层C中各因素（C1～C8）对应于第二层B1的重要性差距不应超过5 倍，第三层C中各因素（C9～C11）对应于第二层B2的重要性差距不应超过4倍。因此，分别引入修正系数c1＝log93、c2＝log95 和c3＝log94，按照前述方法得到修正后的判断矩阵：

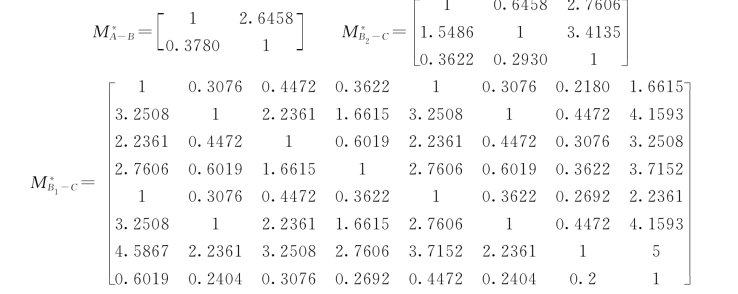
4.建立权重集

表4-13　第二层B中各因素对于A的层次单排序

采用传统AHP对问卷结果进行分析处理，构建权重集，结果列于表4-13、表4-14和表4-15 中。由表4-13 和表4-14可以看出，传统AHP和改进AHP所得的层次单排序结果是一致的。红兴隆分局在进行地下水人工补给实践时，应首选直接补给法。采用直接补给法进行地下水人工补给时，应首选大口井补给方法。采用间接补给法进行地下水人工补给时，应首选激发江河补给方法。由表4-14可以看出，在传统AHP中，直接补给法中大口井补给（C7）权重（0.3526）约为管井补给（C8）权重（0.0211）的17 倍，而引入修正系数后，在改进AHP中，（C7）权重（0.2853）仅为（C8）权重（0.0362）的8倍左右。因此，引入修正系数后，各因素权重间的差距得到了有效的控制，各因素在系统中的重要性更接近于实际。

表4-14　第三层C中各因素对于B的层次单排序

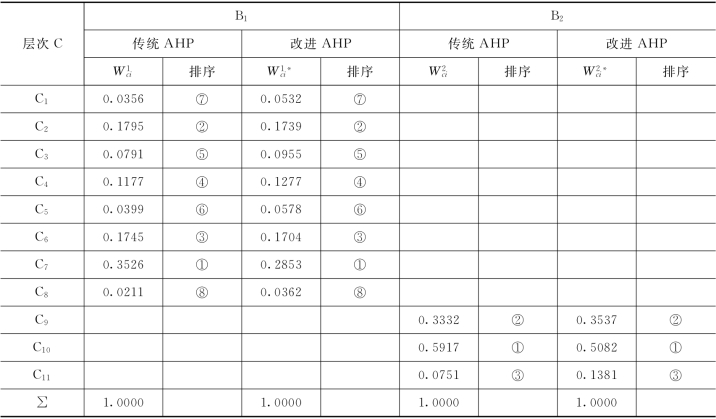
表4-15　第三层C中各因素对于A的层次总排序

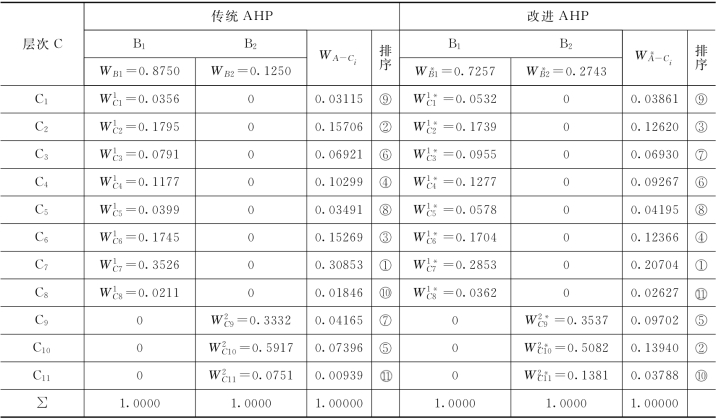
5.一致性检验

按照前述方法，对传统AHP和改进AHP层次单排序和层次总排序进行一致性检验，计算结果见表4-16。

表4-16　一致性检验计算结果

由表4-16 可知，修正前后各判断矩阵的C·R 均小于0.1，符合一致性要求，因此传统AHP、改进AHP的层次单排序及层次总排序有效。