蚁群算法模型及其应用

人与自然是和谐统一的，人类研究自然界的目的之一是利用自然、为人类服务。仿生学就是人与自然统一的桥梁之一。其中蚁群算法引起了学术界的关注，其应用领域不断拓宽，并针对基本算法对其理论进行了较多改进。蚁群算法最初应用于旅行商问题（trave_lingsalesmanproblem，TSP），取得了良好效果，下面就TSP问题具体介绍蚁群算法的基本模型。

式中：allowedk 为蚂蚁k 下一步允许选择的城市；α为信息启发式因子，表示轨迹的相对重要性，反映了蚂蚁在运动过程中所积累的信息在蚂蚁运动时所起的作用，其值越大，则该蚂蚁越倾向于选择其他蚂蚁经过的路径，蚂蚁之间协作性越强；β为期望启发式因子，表示能见度的相对重要性，反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度，其值越大，则该状态转移概率越接近于贪心规则。

根据信息素更新策略的不同，Dorigo M 提出了三种不同的基本蚁群算法模型，分别称之为Ant－Cycle模型、Ant－Quantity模型、Ant－Density模型，其差别在于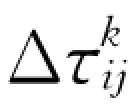（t）求法的不同。

在Ant－Cycle模型中：

式中：Q为信息素强度，它在一定程度上影响算法的收敛速度；Lk 为第k 只蚂蚁在本次循环中所走路径的总长度。(www.xing528.com)

在Ant－Quantity模型中：

在Ant－Density模型中：

式（4-16）和式（4-17）中利用的是局部信息，即蚂蚁完成一步后更新路径上的信息素；式（4-15）中利用的是整体信息，即蚂蚁完成一个循环后更新所有路径上的信息素，在求解TSP时性能较好，因此通常采用式（4-15）作为蚁群算法的基本模型。