根据红兴隆分局水务局提供的853农场1991~2004年的逐月地下水埋深实测序列资料绘制地下水埋深动态变化曲线,见图4-1。从图4-1可以看出,853 农场的逐月地下水埋深呈逐渐增大的趋势。从1991~1998 年的8 年间,地下水埋深增加了2.1m,地下水位年平均降幅为0.3m∕a,这是由于这段时间内水田面积一直维持在1万hm2左右,地下水开采量不大,所以导致地下水位缓慢下降。而从1999 年开始,随着外来水稻承包户的增多,水田面积迅速增加,截至2000年,水田面积发展到2.67万hm2,增长了1 倍多,所以导致地下水位降幅增加,1999~2004年的6 年间,地下水位年平均降幅为0.7m∕a左右。地下水位的持续下降已经严重地破坏了当地地下水资源的供需平衡。
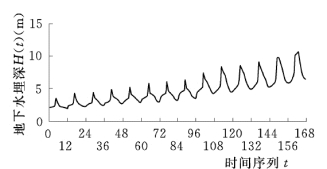
图4-1 853 农场地下水埋深动态变化曲线(1991~2004年)
现以三江平原853 农场为例,根据853 农场1991~2004 年的逐月地下水埋深实测序列资料建立小波随机耦合模型,将2005 年的逐月地下水埋深实测序列资料作为预留检验,对当地地下水埋深动态进行预测。
(一)实测逐月地下水埋深序列平稳化处理
由图4-1 可以看出,853 农场实测逐月地下水埋深序列Ht 为一非平稳时间序列,同时Ht 具有非常明显的以年(12个月)为周期的变化规律,因此可以对序列Ht 进行季节差分。由于Ht 在均值水平上不平稳,因此认为只需对其进行一次差分即可达到平稳,即:
![]()
式中:B 为后移算子。
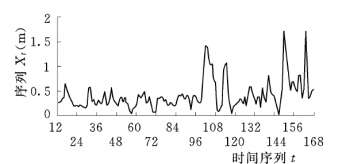
图4-2 853 农场逐月地下水埋深差分序列变化曲线
通过差分,使得逐月地下水埋深序列Ht由非平稳序列转化为平稳序列Xt,见图4-2。
(二)逐月地下水埋深差分序列小波分解与重构
采用前述的A Trous算法,取尺度数P=2,对853 农场1991~2004 年的逐月地下水埋深差分序列Xt 进行分解。由于需要用到边界以外的数据,因此需要进行边界延拓。传统的小波变换边界延拓方法有零值延拓、边界重复延拓、对称延拓、线性延拓、抛物线延拓、平滑延拓、多点拟合延拓、AR 模型预测延拓等[2~4]。信号不同,延拓方法也会不同。经过分析,如果采用边界重复延拓,则在边界以外无法保持序列原有趋势,而如果采用线性延拓,则会夸大序列原有趋势。因此,采用上述两种方法均会产生边界以外数据失真的问题。为很好解决边界延拓问题,本节采用边界重复延拓和线性延拓相结合(各占50%权重)的方法,得到小波分解序列{W1(t),W2(t),C2(t)},见图4-3(a)、(b)、(c)。将各小波分解序列进行叠加,得到重构序列,见图4-3(d)。由图4-3(d)可以看出,重构过程与图4-2 中序列Xt 变化过程完全一致,因此,采用A Trous 算法对853 农场逐月地下水埋深差分序列进行分解是可行的。
(三)小波变换序列成分识别


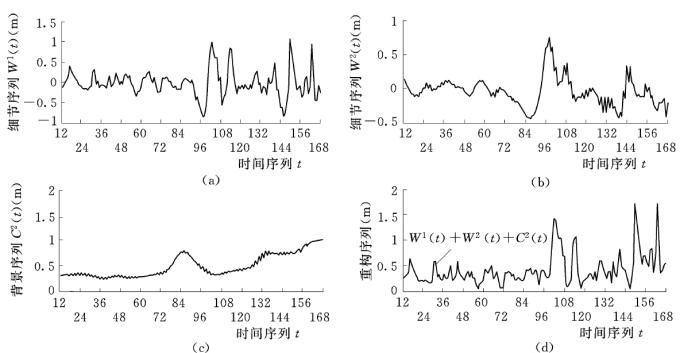
图4-3 853 农场逐月地下水埋深差分序列小波分解与重构
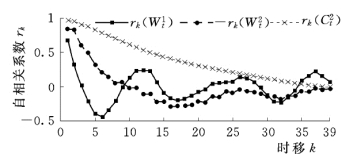
图4-4 各小波变换序列自相关图
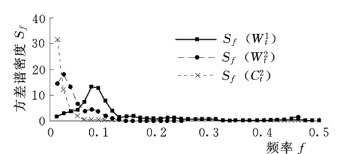
图4-5 各小波变换序列方差谱密度图
(四)小波变换序列互相关分析
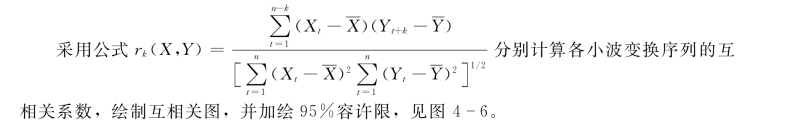
由图4-6 可以看出,各小波变换序列互相关系数基本上落在95%容许限范围以内,且趋近于0。因此,各小波变换序列互相关性较小,可以认为小波变换序列W1(t)、W2(t)和C2(t)两两独立。上述互相关分析结果表明,小波变换序列W1(t)、W2(t)和C2(t)成分单一,比序列Xt 要简单,因此分析和处理Xt 就转嫁为对W1(t)、W2(t)和C2(t)进行处理。
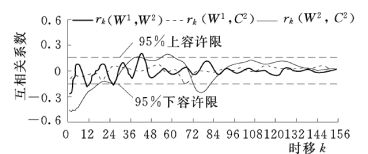
图4-6 各小波变换序列互相关图
(五)建立细节序列W1(t)的随机模型
 (https://www.xing528.com)
(https://www.xing528.com)
对序列W1(t)分别进行自相关分析和偏相关分析,自相关图具有拖尾性,而偏相关图具有截尾性,所以初步判定模型形式为AR(p)模型。参考相关文献,判定模型阶数为1,属于AR(1)模型[5,6]。对AR(1)模型参数进行计算,建立如下自回归模型:
![]()
采用BIC准则对AR(p)模型的阶数进行进一步识别。当p=1 时,BIC达到最小值,BIC(1)=156ln 0.0505+ln156=-460.7321。这说明初步确定的模型阶数为1 阶是合适的。

(六)建立细节序列W2(t)和背景序列C2(t)的自回归模型
细节序列W2(t)和背景序列C2(t)为确定成分,可以借助于水文学中的自回归模型(略去随机变量εt)对序列W2(t)和C2(t)进行描述。
分别对序列W2(t)和C2(t)进行自相关分析和偏相关分析,并采用BIC准测,判定所需建立的W2(t)和C2(t)自回归模型阶数分别为4阶和5 阶。

对于序列C2(t),选定k=1,2,3,4,5(偏相关系数超出95%容许限范围),则略去随机变量εt 的AR(5)模型为:
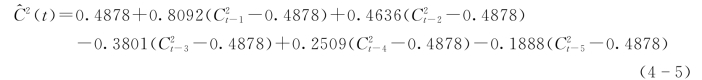
(七)模型组合
将上述各小波变换序列模型进行叠加并还原,就可以得到853 农场逐月地下水埋深小波随机耦合模型,即:

(八)小波随机耦合模型拟合
采用建立的逐月地下水埋深小波随机耦合模型对853 农场1991~2004 年的逐月地下水埋深进行拟合,见图4-7。从图4-7中可以看出853 农场逐月地下水埋深小波随机耦合模型拟合效果良好。
(九)小波随机耦合模型精度检验
采用所建小波随机耦合模型的拟合数据进行拟合效果检验,并采用未参加建模的2005 年逐月地下水埋深实测数据进行试报效果检验,具体计算结果见表4-1。
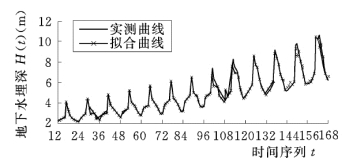
图4-7 853 农场逐月地下水埋深小波随机耦合模型拟合曲线
表4-1 小波随机耦合模型精度检验结果

根据有关文献可知,C、p、E2 和E3 均达到1 级标准,E1 达到2 级标准[7]。因此,所建853 农场地下水埋深小波随机耦合模型拟合效果良好,预测精度较高,可用于预测853 农场未来地下水埋深。
(十)地下水埋深预测
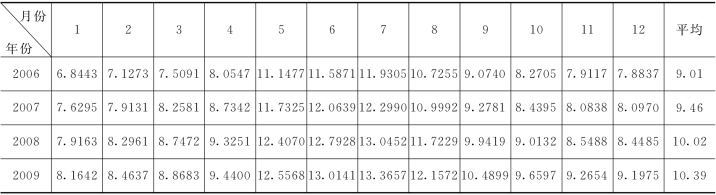
现采用所建小波随机耦合模型预测853 农场2006~2009 年逐月地下水埋深,地下水埋深预测值及预测曲线分别见表4-2 和图4-8。从表4-2 和图4-8 中可以看出,如果仍然采用过去的地下水开采模式,853 农场的地下水位将会持续下降。2006~2009 年地下水埋深年降幅分别为0.62m、0.45m、0.56m和0.37m,未来4年地下水埋深平均年降幅为0.5m左右。因此,853 农场应加大地下水管理力度,以保护当地有限的地下水资源。
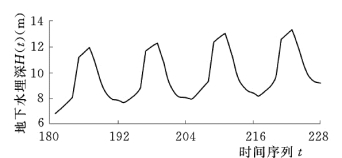
图4-8 853 农场逐月地下水埋深小波随机耦合模型预测曲线(2006~2009 年)
表4-2 853农场逐月地下水埋深小波随机耦合模型预测值(2006~2009年) 单位:m
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




