853农场年降水序列多时间尺度变化特征分析

现以853 农场为例，根据上述小波分析理论，对853 农场年降水实测序列资料进行多时间尺度分析，以了解其不同时间尺度下的详细结构和变化趋势。

（一）资料来源及处理

从红兴隆分局气象台收集到853 农场1959～2005 年的全年降水资料（n＝47）。为处理方便，将年降水实测序列资料进行距平（中心化）处理，并绘制年降水距平序列变化曲线，见图2-23。

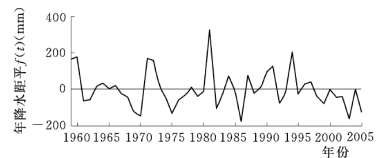
图2-23　853 农场年降水距平
变化曲线（1959～2005 年）

（二）年降水距平序列小波变换

按照前述方法，编程计算853 农场年降水距平序列f（kΔt）（k＝1，2，…，47；Δt＝1）的小波变换系数Wf（a，b）。

（三）年降水距平序列时频分析

按照前述方法绘制853 农场年降水距平序列小波变换系数Wf（a，b）的模平方等值线图（图2-24）和实部等值线图（图2-25），在此基础上进行年降水距平序列的时频变化分析。

1.小波变换系数模平方时频特性分析

由图2-24可以看出不同时间尺度信号能量分布的强弱，其中2～4年时间尺度信号能量变化最强，主要发生在1978～1996 年，振荡中心在1981 年；4～12年时间尺度信号能量变化也较强，主要发生在1959～1988年，振荡中心在1971年；25～37年时间尺度信号主要发生在1959～2000 年；1～2 年时间尺度信号主要发生在1959～1961 年、1968～1973 年、1974～1977年、1982～1985 年、1987～1993 年；其余时间尺度信号能量变化则较弱。

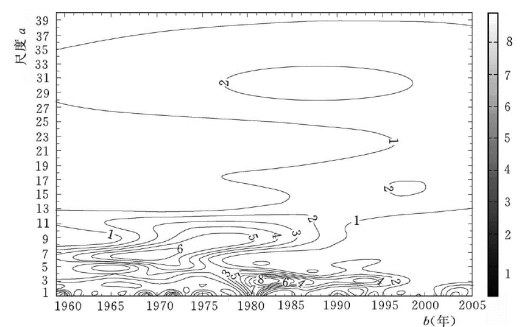
图2-24　853 农场年降水距平序列小波变换系数模平方（×104）等值线

2.小波变换系数实部时频特性分析

由图2-25 可以看出不同时间尺度的变化、正负位相转变点的分布及其位相结构，其中，1～4年、4～12年、25～37 年时间尺度表现最为明显，正负位相交替出现，其中心时间尺度为3 年、7年和30年左右。另外，12～21 年时间尺度也有表现，其中心时间尺度为17年左右。为了进一步说明853 农场年降水距平序列旱、涝交替变化的波动特性，在图2-25 上固定时间尺度a 值（分别取a＝3、7、17、30），作平行于b 轴的切割线，在切割线上取点，作小波变换系数Wf（a，b）的实部（表示为R[Wf（a，b）]）随时移b 变化的过程线，见图2-26。

图2-25　853 农场年降水距平序列小波变换系数实部时频分布

(www.xing528.com)

图2-26　不同尺度下年降水距平序列Morlet小波变换实部变化过程

图2-26 给出了不同时间尺度小波变换系数实部变化过程，现以7年时间尺度为例分析降水量旱涝变化及正负位相转变点的位置。图2-26 （b）给出了7 年时间尺度小波变换系数实部变化过程，可以看出，1960 年以前、1964～1967 年、1971～1974 年、1978～1982 年、1987～1990年、1994～1996 年、2000～2002 年为正位相，表示降水量偏多；而1961～1963 年、1968～1970 年、1975～1977 年、1983～1986 年、1991～1993 年、1997～1999年及2003 年以后为负位相，表示降水量偏少；正负位相转变点在1961 年、1964 年、1967 年、1970 年、1974 年、1978 年、1982 年、1987 年、1990 年、1994 年、1997 年、2000年和2003 年。

（四）年降水序列主要周期分析

利用已经求解出来的不同尺度下的小波变换系数，按照前述方法，通过计算机编程，绘制853 农场年降水距平序列小波方差图，见图2-27。从图2-27 可以看出，小波方差的主要峰值分别出现在尺度a＝3、7、17、30 处，第一峰值为尺度a＝3 所对应的小波方差，说明3 年左右的周期振荡最强，为第一主周期，第二、第三、第四主周期分别为7年、30年和17年。为了识别上述主周期是否具有统计意义，还需要进行显著性检验。

小波方差是否显著，可以采用红噪声或白噪声标准谱进行检验[17，18]。若原序列滞后1的自相关系数r（1）＞0.1，则用红噪声谱检验；若r（1）≤0.1，则令r（1）＝0，用白噪声谱检验。具体检验公式如下：

式中：Pa为红噪声或白噪声标准谱；r（1）为原序列滞后1 的自相关系数；Δt 为原序列时间间隔。

若Var（a）＞P，则说明小波方差所对应的周期是显著的。

经过计算，853 农场年降水序列的一阶自相关系数r（1）＝0.0481＜0.1，所以采用白噪声谱对小波方差进行检验，见图2-27。由图2-27 可以看出，只有3 年和7 年左右的周期超过了95%置信水平，因此，853 农场年降水序列真正的主周期为3 年和7 年左右。17年和30年左右的小波方差虽然也具有一定峰值，但已不明显。

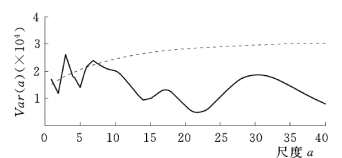
图2-27　853 农场年降水距平序列小波方差（实线为小波方差，虚线为95%置信水平）

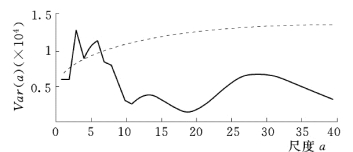
图2-28　853农场主汛期降水距平序列小波方差（实线为小波方差，虚线为95%置信水平）

（五）年降水序列变化趋势分析

图2-26已经给出不同尺度下小波变换系数实部变化过程，通过图2-26　即可分析出各主要时间尺度下853 农场年降水序列的变化趋势。分析较小尺度3 年和7年以及较大尺度17年的变化趋势可以看出，2006～2007 年左右，853 农场的年降水量将处于偏少期，而2008年以后将进入降水偏多期；分析较大尺度30年的变化趋势可以看出，2006～2011年左右，853 农场的年降水量将处于偏少期，而2012 年以后的15 年内，853 农场的年降水量将处于偏多期。

（六）讨论

采用同样的方法对853 农场主汛期（7～8 月）降水序列主要周期进行分析，结果见图2-28。由图2-28可以看出，只有3 年和6 年左右的周期超过了95%置信水平，因此，853 农场主汛期降水序列真正的主周期为3 年和6 年左右。13 年和29 年左右的小波方差虽然也具有一定峰值，但已不明显。由上述分析可知，853 农场主汛期降水序列与年降水序列具有相似的主周期，因此，该地区主汛期降水控制着全年降水。