大气压非平衡等离子体射流案例介绍

1.实验必须满足的一些条件

在等离子体射流的诊断中，为了运用上述理论，必须满足下面的这些条件。

（1）入射光为单色线偏振光，因此需要使用YAG激光器，用以产生窄线宽、高偏振率的激光。

（2）由正负离子导致的散射可以忽略，因为它们的质量相比于电子大得多，由入射辐射场产生的加速度远小于电子的情况。

（3）康普顿效应可以忽略，这需要满足一个入射光子能量远小于电子的静止能量，即hvi≪mec2，使用的激光波长为1064nm或532nm时，均满足条件。

（4）相对论效应可以忽略，这需要满足电子速度远小于光速，即v≪c，对于低温等离子体，满足该条件。

（5）入射光的磁场影响可以忽略。入射光的磁感应强度为B=Ei0/c，洛伦兹力大小为，在v≪c情况下，洛伦兹力远小于电场力，故可忽略磁场影响。

（6）散射光是假定在远场测量的，需要满足观测点到散射点的距离远大于①散射过程中电子的运动距离；②入射光和散射光波长；③观测区域的典型尺寸。

（7）等离子体对于激光是透明的，即激光在等离子体中有很高的传输效率。为了满足这点，入射光频率需要远大于电子等离子体频率。

（8）多级散射可以忽略，这点需要满足入射光经过的等离子体厚度很窄，并且散射概率必须很低（电子密度低）。

（9）EEDF满足麦克斯韦分布和散射光为非相干光。

（10）激光强度必须控制在一个阈值范围下，不能影响等离子体本身（电子密度和电子温度），这点在文献[68]中有详细论述。

2.散射诊断的实验关键

通常，使用同一实验系统来检测瑞利和汤姆逊散射信号。在散射实验之前，应大致估计等离子体参数的大小。为了使给定的激光波长λ0满足α≪1，关于德拜长度或电子密度和温度的一些限制也需要考虑。对于可见光波长的激光器，Te大约为几个电子伏且ne小于1020m-3时，α≪1是有效的。根据前面对三种散射的介绍，在散射实验中需要解决的主要问题如下。

（1）确定好光学几何的位置关系，即入射光波矢方向、入射光电场方向、散射光波矢方向（在确定前三者的方向后，散射光电场方向也能确定）。一般选择正交光路，即θ=φ=90°，因为此时瑞利和汤姆逊散射截面（见式（6.5.12）和式（6.5.28））具有最大值，而空间分辨率达到最佳。不需要的杂散光水平也低于其他角度时的情况。杂散光会使瑞利信号失真，在散射实验中，必须降低杂散光水平。

（2）确定不同散射类型的微分散射截面，汤姆逊散射对应自由粒子，瑞利散射对应重粒子（包含原子和分子），拉曼散射对应多原子分子（常见于N2、O2和CO2）。

（3）确定散射光的光谱形状。因为瑞利散射和拉曼散射的作用对象为重粒子，其在等离子体中的速度远小于电子速度，因此这两种散射中的多普勒效应可以忽略不计，它们的谱线线宽可以近似等于光谱仪的仪器线宽。而汤姆逊散射的谱线宽度将反映电子温度信息。

（4）确定具体的实验条件是否满足公式所需的各种近似条件，如散射光相干性如何。

（5）分析激光对等离子体的扰动。因为在做散射实验时需要聚焦激光，因此在散射区域的激光能量密度会比较高，而高能量密度激光会对等离子体产生加热和光致电离等影响，所以往往需要控制激光能量和聚焦半径，使激光对等离子体的影响足够小，并且保证足够的信号信噪比。

3.汤姆逊信号的捕捉条件

研究具有低电子密度和温度等离子体的两个主要困难是散射强度较弱（在低温等离子体的散射条件下，散射概率约为10-16）和光谱宽度较小（2～5nm），从而导致杂散光会对微弱的汤姆逊信号造成很大的干扰。为了应对这些困难，陷波滤波器和检测器中的多个光谱仪可有效减少杂散光，这两种去除杂散光的方法将在后文介绍。

除汤姆逊散射光谱外，记录的光谱还包含连续的背景，这是由等离子体的连续辐射和检测器中的暗电流引起的。另外，该光谱的中心有很强的杂散光贡献，这是由等离子体周围环境的散射和等离子体中的重粒子散射（瑞利散射）引起的。这些贡献可以从记录的频谱中减去，但是它们的噪声却不能。这种噪声会掩盖汤姆逊光谱本身，因此决定了实验装置的检测极限。从图6.5.6（示意性地显示了记录的散射光谱）可以清楚地看出，汤姆逊信号必须与其他信号源竞争。噪声主要影响汤姆逊光谱的低强度边缘，而杂散光会使光谱的中心失真。两者之间的区域必须足够大，才能根据对测量光谱的拟合准确地确定ne和Te。除噪声外，为了获取足够准确的光谱信号和拟合结果，在一张汤姆逊光谱图中通常至少需要采集100个点，其中中间的20个点由于杂散光需要去除，同时需要满足以下两点原则。

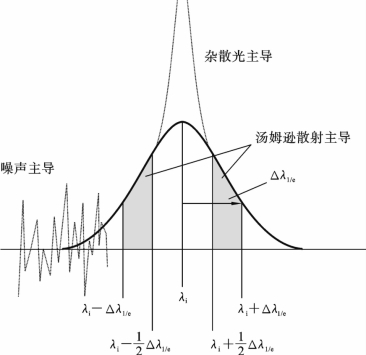
图6.5.6　汤姆逊散射光谱示意图

（1）背景噪声必须小于汤姆逊散射从中心波长到Δλ1/e处的强度（即信噪比为2）。

（2）在中心波长到处杂散光强度要小于汤姆逊散射，具体见图6.5.6。

4.激光散射诊断系统配置

由上文可知，杂散光会使汤姆逊光谱中心部分失真，这对于离周围环境比较近的等离子体或包含在玻璃中的等离子体（高杂散光水平），以及较低的电子密度和温度（汤姆逊光谱较弱和较窄）尤其如此。因此，通常使用三重光栅光谱仪或布拉格光栅陷波滤波器来抑制杂散光。这两种方法都需要与光学器件相关的校准。(www.xing528.com)

（1）三光栅光谱仪（triple grating spectrometer，TGS）。

TGS系统方案如图6.5.7所示，激光聚焦到等离子体区域后，产生散射光由两个消色差平凸透镜收集，成像到TGS的入射狭缝上。由于TGS的入射狭缝为水平方向，这样可以获取散射光在等离子体径向上的分布，所以需要用旋转器将图像旋转到垂直平面。TGS本质上由两部分组成。第一部分由光栅1、光栅2及一个掩模（mask）组成，形成一个陷波滤波器，以从光谱中去除位于中心激光波长的瑞利散射信号。只有散射信号的频谱侧翼可以通过掩模，然后由光栅2重新收集。第二部分由一个狭缝、光栅3及探测相机组成，作用类似传统的单光栅光谱仪。光栅2和光栅3之间的缝隙用以进一步消除杂散光，起到空间滤波器的作用。同时，该狭缝形成了TGS第二部分光谱仪的入口狭缝。光栅3对过滤掉瑞利散射及杂散光信号的散射光重新进行分光，形成聚焦在ICCD相机上的侧翼散射光谱。拉曼和汤姆逊散射信号的测量均需要设置掩模，而在测量瑞利信号时则不需要。为了进一步消除环境的杂散光，可在TGS周围构建一个黑框，并且在光路之间放置黑色屏障。该方法具有较低的电子密度测量下限和较高的时空分辨率，但由于光路经过了三个光栅，散射光的传输效率较低，且由于光学元件较多，所以对校准要求很高。

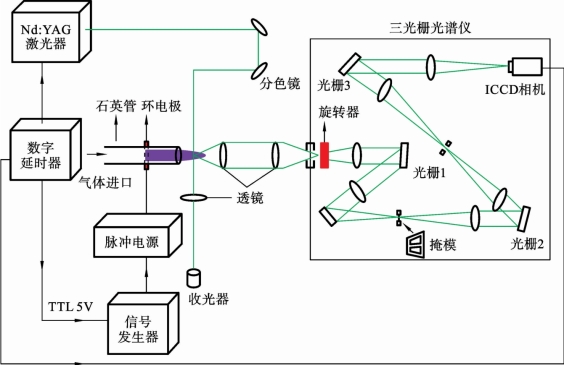
图6.5.7　使用三光栅系统的实验装置示意图

（2）布拉格光栅陷波滤波器（Bragg grating notch filter）。

布拉格光栅陷波滤波器系统方案如图6.5.8所示，通过一个消色差平凸透镜将散射光准直，让准直光通过半高宽为0.2nm（7cm-1）的布拉格光栅陷波滤波片，从而可以把瑞利散射光和杂散光从信号中去除，然后再通过第二个透镜将剩余的拉曼和汤姆逊散射光聚焦到光谱仪中，可有效地采集几乎不失真的汤姆逊信号[69]。对于1eV的汤姆逊散射信号而言，其光谱半高宽在3nm左右，而布拉格光栅陷波滤波片的半高宽仅为0.2nm，这可保证绝大部分的汤姆逊侧翼信号通过滤波片。同时由于瑞利散射信号半高宽近似为光谱仪仪器展宽，远小于0.2nm，这使得陷波滤波片足以充分过滤掉瑞利散射信号和杂散光。由于瑞利散射信号比汤姆逊信号强得多，滤光片必须将瑞利信号减少大约六个数量级才可获得较好的汤姆逊光谱信号。与三光栅系统相比，该方法不会因为反射损耗和附加光栅的效率而导致传输效率大大降低。就杂散光抑制而言，布拉格光栅滤波片具有优越的性能，但对校准要求严格，需要将准直后的散射光对陷波滤波器的入射角调节到光栅衍射角附近，才能发挥出滤波器最好的滤波效果，调节偏角的误差范围需要小于0.1°，因此必须很好地准直散射光[70]。

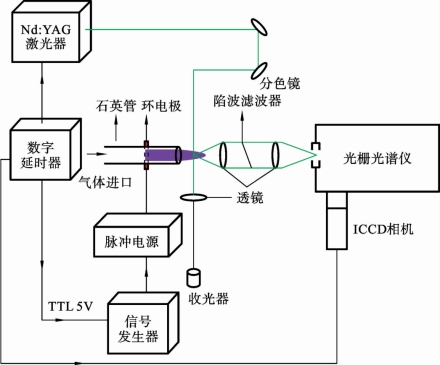
图6.5.8　使用布拉格光栅陷波滤波器的散射系统示意图

（3）单光谱仪与物理掩模配对。

接下来将介绍一个简单的装置，该装置仅使用单个光谱仪与黑色掩模配对即可过滤瑞利信号和杂散光，实验系统如图6.5.9所示。该方法也是利用掩模过滤激光中心波长的瑞利信号和杂散光，但仅使用一个光栅，类似没有第二和第三光栅的三光栅光谱仪系统。散射光通过两块透镜收集到光谱仪中，经过分光后不同波长的散射光聚焦在光谱仪的出口焦平面上。将黑色掩模放置在焦平面上，通过一个精密二维平移台调整掩模位置，使其中心挡板准确挡住激光中心波长的聚焦光，而光谱侧翼信号则可通过挡板两边的开口，由装配有聚焦镜头的ICCD相机采集到。在测量汤姆逊信号时需要在光谱仪入口处放置一个偏振片，用以过滤较强的拉曼信号。这是因为汤姆逊散射是偏正的，且其偏正方向与入射激光一致，而拉曼散射则是非偏正的。在测量拉曼信号时则将偏振片换成一个长通滤波片，以提高校准的准确度。Chen[71]将这种检测策略扩展到中等气压和1012cm-3电子密度的情况。Van de Sande[72]和Brehmer[73]等人使用了类似的方法，即在ICCD的正前方放置了一条纸条充当掩模的作用。此外，根据放电中遇到的杂散光量，可以将掩模加工成特定的宽度，这使得该设置可以更灵活地测量多种类型的放电装置。由于该方法使用的光学元件更少，所以散射信号的传输效率更高。并且只需要一个常见的单光栅光谱仪，无须复杂的光路配置和校准。然而，该方法对杂散光的过滤有限，大量的杂散光可能会掩盖住汤姆逊信号。因此，该方法比较适合杂散光水平较低的中低气压放电。在高气压放电中则需要更高的电子密度，以使汤姆逊信号相比于杂散光强度足够大。

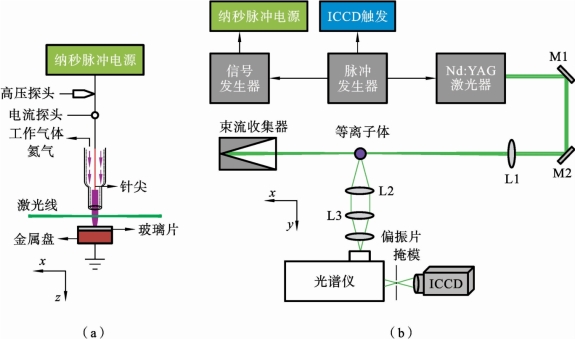
图6.5.9　使用单光谱仪与物理掩模配对的测量装置示意图

（a）等离子体射流示意图；（b）散射光路图

以下以He等离子体射流为例，介绍散射信号处理方法。在去除瑞利散射和杂散光后，探测器实际采集到的信号由三部分组成：汤姆逊散射、N2和O2上的拉曼散射以及背景光。它们的光谱是重叠的，借助Matlab®编写的专门设计的软件，能够拟合这些重叠的信号并将其分离。

汤姆逊光谱使用式（6.5.18）计算，拉曼光谱使用式（6.5.36）计算。假定仪器展宽对汤姆逊信号半高宽的影响可忽略不计，则没有卷积应用于汤姆逊频谱。汤姆逊、N2拉曼和O2拉曼这三者的贡献是分别计算求和的，并添加恒定的背景信号C，所以总信号为：

其实，使用分气压pN2+pO2和混合比pN2/pO2代替pN2和pO2作为拟合参数更为方便。拟合参数的总个数为6，即ne、Te、Trot、pN2+pO2、pN2/pO2和C。

为了获得压力和密度的绝对值，必须对信号进行绝对校准，确定校准系数fLPiΔΩ。这是通过拟合无等离子体的环境空气的拉曼光谱来完成的。在这种情况下，温度和气压均可确定，根据理想气体方程，分子的绝对密度可以确定。应注意在每次汤姆逊测量之前和之后都测量转动拉曼光谱，并将其平均以解决激光能量可能存在的漂移。

接下来给出了使用激光散射技术进行大气压非平衡等离子体诊断的一些典型结果。

对于纳秒脉冲电源驱动的等离子体，实验装置图如图6.5.9所示。利用方法3测得的拉曼和汤姆逊光谱示例图如图6.5.10、图6.5.11所示。

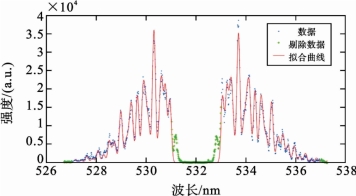
图6.5.10　拉曼散射光谱实例

Trot=（290±5）K，pN2+pO2=1.01×105Pa，N2/O2=80.2%/19.8%（未发表）

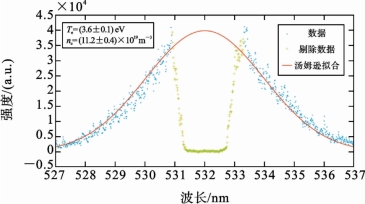
图6.5.11　汤姆逊光谱示例图

Te=（3.6±0.1）eV，ne=（11.2±0.4）×1019m-3（未发表）