等离子体射流中的拉曼散射和汤姆逊散射强度校准

拉曼散射是入射光子与分子之间发生的非弹性散射，此过程中会经过振动态或转动态的跃迁，从而导致散射光发生特定的波长偏移。典型的拉曼散射光谱见图6.5.5。可以看到，拉曼光谱显示大量窄线，它们对应于不同的转动、振动跃迁而处于不同的波长偏移。拉曼散射光的相位相对于入射光是随机分布的，所以拉曼散射始终是非相干的，总散射功率就是单个散射粒子的散射功率总和。在等离子体射流的激光散射诊断中，拉曼散射可用于测量分子的转动温度，同时校准汤姆逊散射强度。下面对拉曼散射的散射截面公式进行推导，并讨论总散射功率表达式。

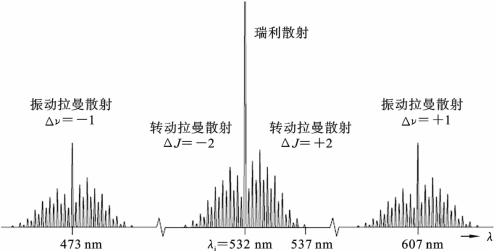
图6.5.5　典型的拉曼散射光谱

1.线性分子的拉曼散射

这里先假定散射分子（O2、N2和CO2）为简单线性分子，并且所有的分子处于振动态基态，这个在低温条件下（小于1000K）是近似满足的。由于光谱仪的范围限制，这里仅考虑转动拉曼散射。拉曼散射光谱的不同峰值波长为其中，λi为入射光波长，J为转动量子数，B为基态振动态的转动常数，取决于粒子种类（见表6.5.1）。h和c分别为普朗克常数和光速。

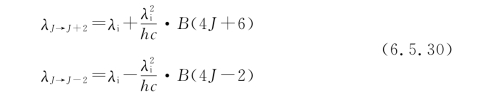
对于J→J′的跃迁过程，参考式（6.5.4），其散射功率可表示为

其中，nJ为处于转动态J的分子密度。对于正交散射的情况，即θ和φ均为90°时，J→J′的拉曼散射微分截面为

γ为分子的各向异性（见表6.5.1），bJ→J′是Placzek-Teller系数，表达式为

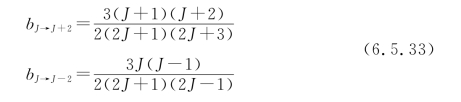
假定处于J态的粒子密度遵循玻尔兹曼分布，则有

其中，nmol是分子密度，gJ为统计权重因子（见表6.5.1），Trot为转动温度，Q为配分函数，可近似表示为(www.xing528.com)

其中，I是核自旋量子数（见表6.5.1）。最终根据式（6.5.31），可以获得拉曼散射的总功率为

拉曼光谱的形状函数Sλ（λ-λJ→J′）一般远小于光谱仪的仪器轮廓，所以实际计算中用光谱仪的仪器函数代替（与瑞利散射类似）。

上述推导过程是基于假定所有分子都处于振动基态的情况下，在振动温度较高的等离子体射流中，还需考虑振动激发态的粒子损耗。通常第一振动激发态与振动基态的分子密度比为

其中，E10是第一振动带的能量，见表6.5.1。

表6.5.1　分子常数

2.汤姆逊散射强度的校准

在散射实验中，如果要获取散射粒子的绝对密度，则需要得到散射信号的绝对强度，这便需要确定一系列校准常数（fLPiΔΩ）。相比于自由电子，在实验室中更容易获得确定分子密度的气体环境，因此常用已知气体组分的瑞利或拉曼散射来对汤姆逊散射的绝对强度进行校准，从而获得等离子体中自由电子的绝对密度。而用拉曼散射进行校准相比于瑞利散射有以下优点。

（1）瑞利散射和杂散光的波长相同，分离的难度较大。而拉曼散射相对于杂散光波长会有明显的偏移，分离起来更加容易。

（2）虽然瑞利散射截面比汤姆逊散射小得多，但瑞利散射强度远大于汤姆逊散射。由于探测器的饱和效应，在测量瑞利散射和汤姆逊散射时所使用的相机设置参数会有较大差距，而且测量汤姆逊散射时还需设置额外的滤波单元，这些都会引入较大的误差。而拉曼散射强度与汤姆逊散射强度相近，且无须改变实验配置，准确性能够大大提高。

因此通常用拉曼散射来进行校准。在等离子体射流的诊断中，通常采集室温下纯N2或空气环境中的拉曼散射光谱，这种情况下转动温度和分子密度均可由实验环境中的气压和温度确定。通过式（6.5.36）对光谱仪采集到的散射光谱进行拟合，即可确定校准常数，从而标定等离子体中自由电子的绝对密度。