汤姆逊散射在大气压非平衡等离子体射流中的物理基础

汤姆逊散射是入射光子与空间中的自由电子发生的散射。入射电磁波引起自由电子以入射波的频率振荡，被加速了的自由电子随即产生偶极辐射，此即为汤姆逊散射。如6.5.1节所述，散射截面及散射光谱与粒子速度分布之间的关系十分重要。在本节中，将通过分析单个电子的散射过程，推导出汤姆逊散射的散射截面公式，并讨论满足麦克斯韦电子能量分布函数（EEDF）的电子散射光谱形状。

1.单个电子散射

入射激光一般为线性偏振单色平面波，其电场表达式为

设单电子的速度为vj，位置在rj（t），该电子在入射光电场下的加速度为

根据电动力学，加速电子在r（t）处产生的电场为

这里，R=r-rj=Res，R表示电子与观察点r间的距离，位置向量关系如图6.5.2所示。

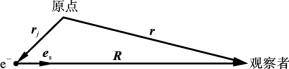
图6.5.2　位置向量定义

需要注意的是t时刻在观测点探测到的电场实际是由t′=t-R（t′）/c时刻位置上的电子产生。定义经典电子半径为

假设电子速度v≪c，则R（t）≈R（t′），因此散射电场表达式可化为

散射几何方向如图6.5.3所示。

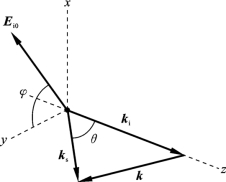
图6.5.3　散射几何方向

由此，散射波的坡印廷矢量为

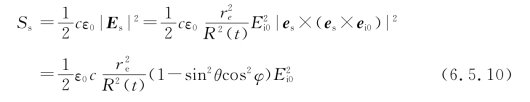
在距离电子R（t）的位置上，散射光在单位立体角中流入的能量为

根据，对于单个电子，N=1，而，将其代入式（6.5.11）可得

一般散射实验中采用正交光路结构，即θ=φ=90°，则。

2.满足麦克斯韦EEDF的电子散射

等离子体产生的汤姆逊散射电场是在散射区域里的每个电子产生的散射电场向量和。如果这些电子产生的散射电场相位彼此是不相干的，那么产生的散射光是非相干光。对于非相干光，总散射功率可表示为每个电子的散射功率的简单叠加。参考式（6.5.4）可得(www.xing528.com)

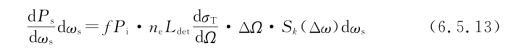
Sk（Δω）dωs表示一个散射光子的频移落在Δω附近dωs范围内的概率，由式（6.5.2），令vk=Δω/k，上述概率等于一个电子在k方向上的速度分量落在vk附近dvk区域里的概率。

结合式（6.5.3），k=2sin（θ/2）ki=和，用波长来代替频率，上式改写为

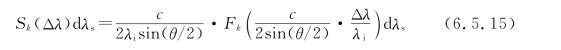
因此光谱分布函数的形状跟速度分布函数一致。若速度分布符合麦克斯韦分布，则有

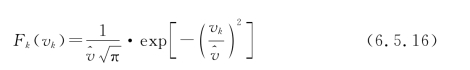
其中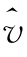，是电子的最可几速率

其中，kB、me和Te分别为玻尔兹曼常数、电子质量和电子温度。由此，式（6.5.13）可改写为

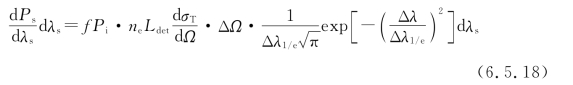
其中，Δλ1/e是散射光谱的1/e半宽值，表达式为

由此可推出电子温度表达式

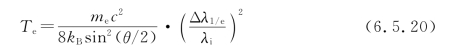
假若取正交散射坐标系（θ=90°），入射光波长为532nm，则电子温度为

在非相干散射和麦克斯韦速率分布情况下的汤姆逊散射光谱简图如图6.5.4所示，通过散射光谱的1/e半宽值可获得电子温度Te，在经过校准确定式（6.5.18）中的fLdetPiΔΩ的情况下，将测得的散射光信号强度代入式（6.5.18），并结合式（6.5.12）和式（6.5.19）得到的dσT/dΩ和Δλ1/e，即得到电子密度ne。

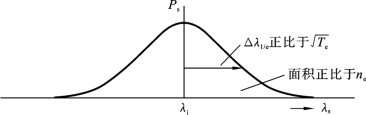
图6.5.4　在非相干散射和麦克斯韦速率分布情况下的汤姆逊散射光谱简图高斯谱的面积和宽度分别与ne和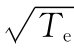成正比

上述推导是建立在散射光为非相干光的基础上的，而散射光的相干性通常用散射参数α来描述：

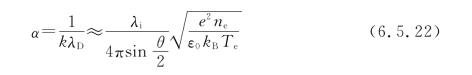
当α≪1时，散射光可以看作非相干光。对于大气压低温等离子体，电子温度Te通常在1～10eV区间，电子密度在1011～1015cm-3区间[65]，在正交光路条件θ=90°和λi=532nm下，当电子密度≤1014cm-3，散射参数α最大值为0.08，此时可以将散射光看作非相干光。而当电子密度达到1015cm-3时，散射参数α最大值为0.25，此时散射光呈现弱相关性，需要对式（6.5.14）中的Sk（Δω）进行修订，有

其中，Rω（Δω/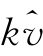）是等离子体色散函数的实部，即