激光散射简介：大气压非平衡等离子体射流物理据

当一束激光照射到等离子体时，等离子体中重粒子的束缚电子和空间中的自由电子会在激光电场的作用下产生加速振荡，受到加速振荡的电子会向空间中各个方向发出散射光，这个过程即为激光散射。

根据散射前后光子能量是否发生变化，光散射分为弹性光散射和非弹性光散射。一束频率为ωi的入射光照射在物体上，如果散射光的频率ωs等于入射光的频率ωi，称其为光的弹性散射，即散射前后入射光子和散射光子的能量没有发生变化。如果散射光的频率相对于入射光的频率发生了偏移，则称其为光的非弹性散射，即散射前后光子能量发生了变化。由等离子体中的自由电子导致的散射称为汤姆逊散射。由原子、离子和分子的束缚电子导致的散射称为瑞利散射。它们都属于弹性散射。另外，由分子导致的散射会引起转动能级或振动能级的跃迁，这种散射称为拉曼散射，属于非弹性散射。

典型的散射过程示意图如图6.5.1所示。当激光通过某个散射体时，设入射激光的横截面积为A，在散射区域内，n为散射粒子密度，散射区域的长度为Ldet，则该区域内粒子总数为N=nLdetA。设σ为粒子的激光散射截面，那么激光的散射概率可表示为Nσ/A=nLdetσ。散射功率Ps可表示为

其中，f为考虑到光学镜片和相机的传输效率的常数，Pi为入射功率。

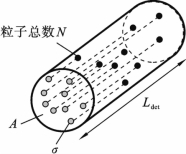
图6.5.1　典型的散射过程示意图

散射光的波长ωs可能会与入射光波长ωi不同，这是因为散射粒子自身存在运动速度，导致了两种多普勒频移。一种是散射粒子在入射光方向上的运动分量，这使得散射粒子实际“见到”的入射光频率为ωp=ωi-ki·v；第二种是散射粒子相对于观察方向也即散射方向上的运动，这使得观测者实际观测到的散射光频率为ωs=ωp+ks·v。ki和ks分别为入射光和散射光的波矢量。这里定义散射波矢为k=ks-ki，两种多普勒频移可以相互叠加或抵消，这取决于散射粒子速度v相对于散射波矢的方向。因此最终导致的散射光频移为(www.xing528.com)

频移大小为粒子速度在散射波矢方向上的分量和散射波矢大小的乘积。对于散射粒子v≪c，可以认为ks≈ki，那么散射波矢大小定义为

其中，θ为散射角（即ki和ks的夹角）。从式（6.5.2）可以明显看出，不同粒子的散射光的频率分布与在k方向上的速度分布直接相关。这使得激光散射适合于测量等离子体中粒子的速度和能量分布，以及与该分布有关的参数，例如散射粒子的温度。如果能量分布呈麦克斯韦分布，则散射谱具有高斯线型。通常用比式（6.5.1）更加精细的表达式来描述散射过程，即

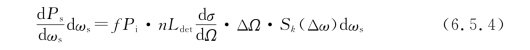
这里用微分散射截面和立体角的乘积代替了式（6.5.1）中的散射截面σ，这是因为在不同的散射方向上，散射截面是不一样的。另外该公式引入了频谱分布函数Sk（Δω）来描述散射光谱的形状轮廓。在非相干散射的情况下，频谱分布函数对于总散射功率影响并不重要，因为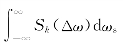=1。