大气压等离子体射流：OH和O的诊断与标定方案

在具体的LIF实验中，探测器测量到的只是待测粒子辐射荧光的相对强度，而从辐射荧光的相对强度推导出绝对粒子密度的过程称为绝对密度标定。绝对密度标定关键有两点：一是确定式（6.4.4）中的校准常数η，二是建立绝对密度计算模型。

校准常数取决于观测立体角和光路几何结构，反映的是荧光采集系统的采集效率。若是从光学器件参数和几何光路尺寸直接确定该系数的具体值，则会在求解绝对密度中引入很大的误差。因此常采取的方法是保持待测粒子的LIF实验光路不变，引入已知密度的气体，进行相似的激光实验（LIF或散射实验），从而推导该系数取值或在方程中消除该参数。比如在标定氦气等离子体射流产生的NO的密度时，就可以在氦气中人为地混入确定密度的NO，通过测量该混合气体的LIF相对强度，推导出校准常数。

原子的单光子吸收LIF的密度计算模型已在6.4.1节中进行了分析，但对于分子的单光子吸收LIF还存在振动能级和转动能级的影响，需要建立更复杂的计算模型。此外双光子吸收LIF由于激发过程的不同，也需要对模型进行一定的调整。下面将介绍等离子体射流中十分重要的OH自由基和O原子的LIF诊断及标定方案。

1.OH自由基的诊断及标定

由于OH是活性很高的短寿命分子基团，在大气中无法稳定存在，无法获得含有确定密度OH的混合气体，因此针对这种短寿命分子基团，国际上主要使用空气的瑞利散射来确定校准常数。在LIF实验中常采用正交系光路结构，即入射激光沿x轴传播，线性偏振方向为z轴，探测器检测方向为y轴，彼此正交。在保证与LIF实验相同的光路条件和探测器参数配置下，假定测量区域内激光密度保持不变，则测得的瑞利信号强度可表示为

其中，λR为瑞利散射激光波长，通常调节为308nm，与荧光波长一致；η是与LIF实验中相同的校准常数；t（λR）和G（λR）分别为光学选择单元对瑞利散射波长的透过率和探测器对瑞利散射波长的量子效率；VR为散射区域体积；W L为激光在测量区域的能量截面密度（W L=EL/AL）；NR为散射粒子（空气分子）密度，由公式决定；为瑞利散射的微分截面（单位：m2/sr），在正交光路几何配置下，瑞利散射的微分截面可表示为

其中，σ为散射物质的总瑞利散射截面（单位：m2），由查表和插值法确定[47]，在288K，大气压条件下，空气对308nm的散射截面为5.05×10-30m-2；ρ0为入射光的水平-垂直偏振光比率，对于一般的Nd：YAG激光器该值一般在0.01左右。

激光诱导荧光测量射流中的OH自由基时，LIF过程会同时受到猝灭过程（quenching）、振动能级转换（vibrationalenergytransfer，VET）和转动能级转换（RET）的影响，如图6.4.3所示。因此测量到的OH自由基的荧光是由不同的光谱带组成的，这与激光诱导荧光测量原子时的单一（或多条）独立的荧光谱线不同。目前国际上广泛采用282nm激发机制来进行OH-LIF实验，对应的能级迁移为，通常使用P1（2）、P1（3）和P1（4）等具有较高吸收系数的激发谱线。激发态OH通过自发辐射产生314nm的OH（A→X，1→1）振动转动谱带。与此同时，由于VET和RET的作用，会出现308nm的OH（A→X，0→0）谱带。因此探测器测量到的是几个荧光谱带的叠加信号，同时由于分子的振动和转动能级繁多，而且振动能级和转动能级间的跃迁过程及速率与周围碰撞粒子的种类、温度等相关，导致OH荧光信号的分析以确定绝对密度需要考虑较多的因素。

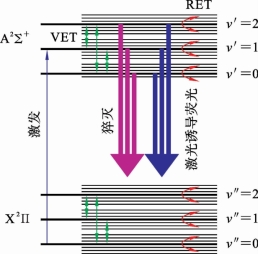
图6.4.3　OH自由基激光诱导荧光信号时需要考虑的几种“竞争”机制[48]

其中，激发表示激光激发过程，RET和VET分别是OH自由基转动和振动能量传输过程，猝灭表示由于碰撞导致高能态OH（A）消失的过程，激光诱导荧光表示自发辐射产生荧光的过程

为了准确地计算推导出等离子体射流中的OH绝对密度，以上提及的（图6.4.3中所示）竞争过程都需要在信号分析中考虑。根据式（6.4.4），假定OH密度在测量区域内密度均匀分布，则探测器测量到的OH自由基荧光强度SLIF可以用以下公式表示：

式中，λij是高能级i跃迁至低能级j辐射的荧光波长，Aij是自发辐射系数，Ni（）t是t时刻处于高能级i的OH自由基密度。假定在测量区域内OH密度均匀分布，则通过瑞利散射标定，结合式（6.4.6）和式（6.4.8）可以得到

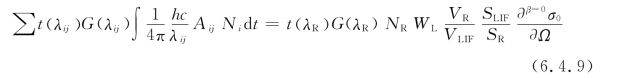
在式（6.4.9）中，建立不同能级下Ni的速率方程十分重要。目前国际上建立速率方程的方法主要有光谱拟合法和精简能级法。下面将具体介绍这两种方法。

光谱拟合法采用光谱仪作为波长选择单元，测量OH的荧光光谱，借助LASKIN等光谱模拟软件进行拟合分析（如图6.4.4所示），在拟合的光谱中挑选一条合适的荧光谱线，获取相关能级的衰减速率，从而推导计算出基态OH绝对密度。以P1（2）激发谱线为例，定义被激发的低能级为能态1，激发的高能级为能态2，能态2自发跃迁至OH（X）的一个振动转动能级为能态3，那么能态2的密度可以通过式（6.4.9）求得：

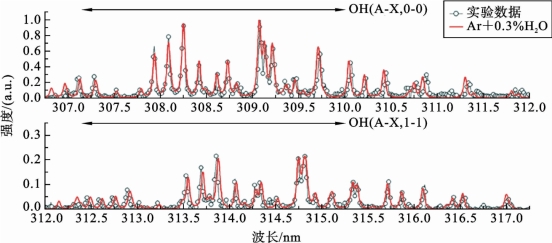
图6.4.4　LASKIN对Ar射流中混合0.3% H2O时测量的OH荧光光谱的拟合[48]

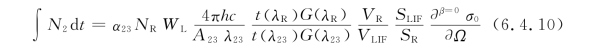
式中，α23表示能态2跃迁至能态3产生的荧光强度与测量到的总荧光强度的比例，可以通过LASKIN程序模拟得到。能态1和能态2的密度时间变化可以由以下速率方程组表示：

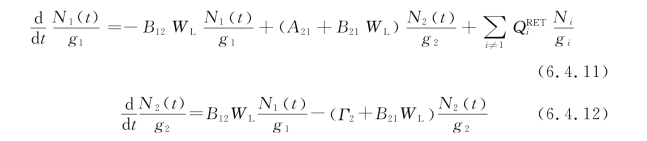
式中，gi是相应能级的统计权重，是转动能量传输速率，数量级为109s-1。Γ2是能态2在各种机制作用下的总消失速率，包括碰撞消失、自发辐射、转动及振动能量传输过程，该参数由LASKIN程序计算得到。结合式（6.4.10）～式（6.4.12），可以求得能态1的密度。如果OH X，v″（）=0的转动能级数量分布达到热平衡状态，则可以通过玻尔兹曼分布函数（式（6.4.5））最终得到OH（X）的绝对密度。

虽然光谱拟合法可以得到很好的准确度，但由于光谱反应十分复杂，反应方程繁多，编写光谱拟合软件困难很大。而且由于需要采集光谱，装置也更加复杂。因此很多课题组采用了精简能级的方法。

精简能级法在不同的实验条件下，对OH的荧光过程做出不同程度的假设，将OH的LIF过程中的多个转动态进行合并，从而达到用很少的能级数量来描述整个LIF过程的目的。该方法使用ICCD搭配滤波片即可使用，而无须采集荧光光谱。目前国际上已经提出了2级到6级等不同数目的精简能级模型，其中6级模型的准确率较高，同时考虑到了VET和RET过程，如图6.4.5所示。但在常见的大气压射流等离子体中，OH的RET速率远高于VET速率和猝灭速率，在激光激发和辐射荧光的时间尺度上，转动态分布接近平衡条件。这样便可只考虑4个振动态而不用考虑转动态的影响。因此在6级模型基础上简化的4级模型在等离子体射流中应用较为广泛。

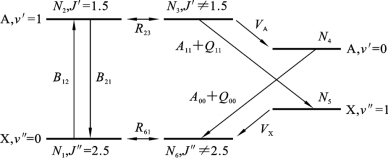
图6.4.5　详细的6级模型的辐射和碰撞过程[49]

详细的4级模型的能量传输过程如图6.4.6所示，包含了基态能级的激发和受激辐射，自发辐射及碰撞猝灭和振动能级的能量转移。不同能级粒子密度的微分方程组为

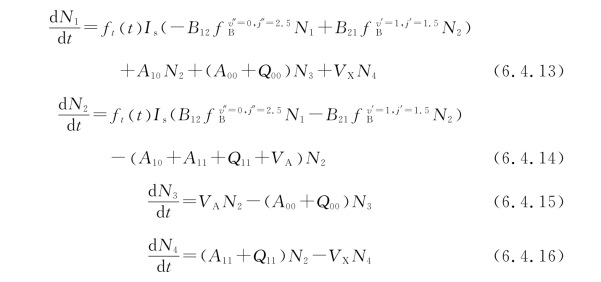
其中，Ni表示位于能级i的粒子密度（单位：m-3），Bij是能级i到能级j的爱因斯坦B系数，是在振动能级v和总角动量j的玻尔兹曼因子（与气体温度相关），VA和VX分别为激发态和基态的振动弛豫速率，Aij和Qij分别为激发态的振动能级i到基态的振动能级j的自发辐射系数和总猝灭速率（包括电子态猝灭和VET猝灭）。

碰撞猝灭和VET反应速率计算公式为(www.xing528.com)

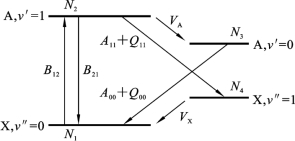
图6.4.6　详细的4级模型的辐射和碰撞过程[49]

其中，ki是OH与碰撞粒子i的反应速率系数，Ni是碰撞粒子i的密度。

在该模型中，在激光脉冲期间气体温度基本保持恒定。而且除了A11和A00外忽略了其他的自发辐射，这是因为其他自发辐射速率要小两个数量级以上。采用滤波片采集308nm和314nm谱带的荧光信号，则根据式（6.4.8），荧光信号强度可表示为

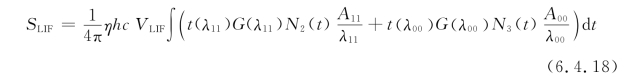
在已知校准常数η的条件下，联立式（6.4.13）～式（6.4.18）即可求得OH自由基的绝对密度。模型中的常量参数见表6.4.1。

表6.4.1　4级模型常量参数表（取值来源于文献[50]）

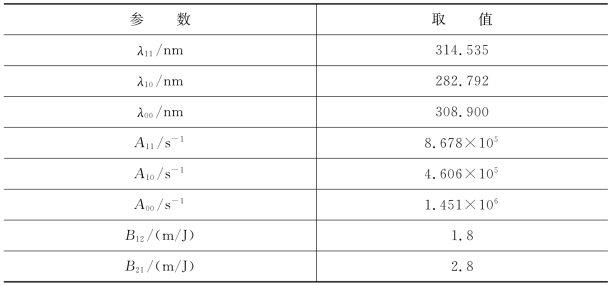
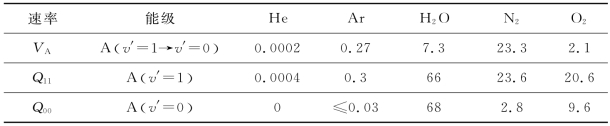
表6.4.2列出了OH在300K条件下与常见碰撞粒子碰撞猝灭速率系数和振动弛豫速率系数。基态VX的振动弛豫率一般比激发态VA的VET速率小2个数量级。

表6.4.2　300K条件下各类反应速率系数（单位为10-17m3/s，取值参考文献[49，51]）

除了使用上述方法对OH绝对密度进行标定外，还有一种基于化学模型标定的方法。该方法无须通过瑞利散射对荧光信号公式中的校准常数η进行测量，而只用测量OH-LIF相对荧光强度在等离子体放电停止后的衰减曲线。根据OH自由基的衰减反应机制，建立OH粒子密度的衰减速率方程，并与荧光强度衰减曲线进行拟合，从而获取基态OH绝对密度的估算值。目前此方法已成功用于He或Ar为工作气体的脉冲放电射流中，这是因为这类射流中的OH主要损失过程少，反应速率容易获得，在更复杂的例如分子气体的实验条件下此方法便不适用了[52]。

2.O原子的诊断及标定

O原子绝对密度使用双光子吸收激光诱导荧光（TALIF）来测量。TALIF法非常方便，因为基态O的单光子激发将需要真空紫外（VUV）波段的光，对于实验环境的要求非常苛刻。O原子的TALIF中通常使用两个225.6nm的激光光子来激发到3p3P1，2，0能级，观测跃迁至3s3S能级的荧光（845nm），其能级图如图6.4.7左侧所示。由于TALIF荧光信号与激光强度的平方成正比，所以无法使用瑞利散射来获取校准常数。因此通常采用氙气（Xe）校准，这是由于O和Xe的激发波长和荧光波长的相似性，因此实验条件保持不变，如图6.4.7右侧所示。Xe的TALIF测量通常使用224.3nm的激发波长和835 nm的荧光波长。

对时间、体积、荧光波数和激发波数积分的TALIF信号强度可表示为

其中，n1（单位：m-3）表示O或Xe基态能级的粒子密度；C表示标定系数，取决于观测透镜、波长选择单元和探测器的传输效率；G（2）=2是光子统计因子；σ（2）（单位：m4·s）是双光子吸收截面；a是观测的荧光跃迁过程的分支比（branching ratio）；ħω（单位：J）是激光的光子能量；I（t，r）（单位：W/m2）是激光强度对时间和空间的函数。由于O和Xe的激发波长十分接近，假设激光强度分布的轮廓是恒定的，上式的积分项可表示为

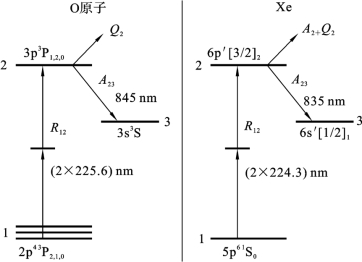
图6.4.7　O原子和Xe的TALIF相关能级示意图

其中，c表示激光强度分布的常数，E表示用激光能量计测得的脉冲能量（单位：J）。此假设对TALIF系统的稳定性要求很严格，必须保证对O和Xe的测量光路不变。

在大气压下，碰撞猝灭会大大减少从激发态到基态跃迁的自然寿命，因此碰撞猝灭速率必须考虑在式（6.4.19）中的分支比中：

其中，A23表示能级2到能级3的自发辐射速率，是能级2的总辐射衰减速率，与能级2的自然寿命有关，A2=。对于O原子，A23/A2=1；对于Xe，A23/A2=0.733。qi表示激发粒子与碰撞粒子i的猝灭系数，ni是碰撞粒子密度。对于Xe的TALIF测量，可以人为预设混合气体比例，从而很容易确定ni的值。但是对于等离子体射流中的O原子测量，由于不同位置周围空气的渗入和等离子体化学反应的产物等影响，确定ni的具体数值是比较困难的，因此常使用拟合O原子荧光寿命来获得能级2的总衰减速率，=τ-1。首先通过实验获得荧光时间分辨信号，然后通过测量瑞利散射信号获得激光脉冲的时间演变函数的平方。通过将一个指数衰减函数和进行卷积拟合，这个指数衰减函数的衰减时间即为τ。注意只有当荧光持续时间大于激光脉冲持续时间时才可用此实验方法，否则只能使用理论计算法获得碰撞猝灭速率。

低能级O3p4PJ和高能级O3p3PJ′都根据轨道角动量量子数分为三个能级，J=2，1，0和J′=1，2，0。高能级J′间距离小于激光线宽，因此在激发和荧光过程中无法区分；但是低能级的能量间距远大于激光线宽，因此被细分成了3个激发波长（2×225.685）nm、（2×225.988）nm和（2×226.164）nm。经过Xe标定的基态nJ绝对密度为

其中，σ（2）和a对于所有3个基态J能级是相等的，并且。CXe/C近似等于探测器在844.68nm和834.68nm的量子效率之比。基态原子的总密度是3个J态粒子密度之和，即

标定所需的O和Xe相关能级的自然寿命和碰撞猝灭速率系数如表6.4.3所示，其中猝灭速率是在室温条件下的数值。

表6.4.3　O和Xe的相关能级的自然寿命和猝灭速率常数[53，54]